Miért esik az Arrhenius-egyenlet mindig az "exponenciálisan növekvõ" tartományba, amikor a kémiai kinetikát vizsgáljuk?

---

A fordítás Harvey F. Carroll írása alapján készült (Journal of Chemical Education, 1998., 75. k., 9. sz., 1186–1187. o.),  a JCE engedélyével. A Journal of Chemical Education lapjait a http://jchemed.chem.wisc.edu/ címen érheti el.

---

Az általános kémiai tankönyvekben a sebességi állandóról rendszerint azt mondják vagy azt tételezik fel, hogy a hõmérséklet exponenciális függvénye, majd azt állítják, hogy ezt a jelenséget az Arrhenius-egyenlet önti matematikai formába:

ahol k a sebességi állandó, A a preexponenciális vagy frekvenciafaktor, E_a az aktiválási energia, R=8,315 Jmol^–1K^–1 a gázállandó, T az abszolút hõmérséklet.

Aki az Arrhenius-egyenlet tulajdonságait akarja felvázolni a hallgatóknak, valószínûleg a következõ egyszerû exponenciális egyenletet használja modellként:

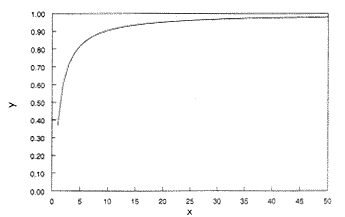
Általában feltételezzük, hogy ez egy exponenciális növekvõ függvény. De amint az 1. ábra mutatja, ez a függvény 1-hez tart aszimptotikusan, miközben x tart a végtelenhez, és a grafikonon megadott tartományban egyaltalán nem fest exponenciálisan növekvõ függvényként.
 

1. ábra. Az nagy x-értékek esetén	2. ábra. Az , ha x 0 é s 1  közé esik

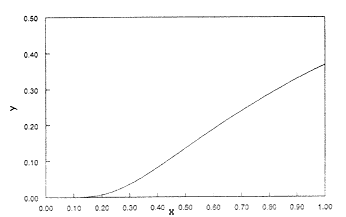
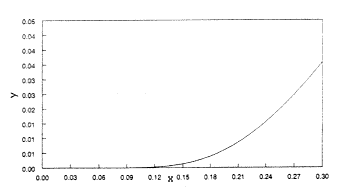
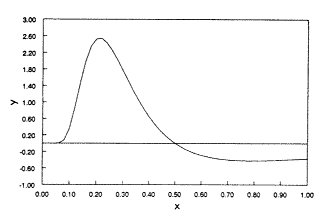
Ha azonban x 0 és 1 között változik, akkor úgy látszik, hogy a görbének "exponenciálisan növekvõ"¹ tartománya és inflexiós pontja is van (2. ábra). Még kisebb x-értékeknél jól látszik, hogy a görbe "exponenciális" (3. ábra).

Az elsõ derivált, amelynek az inflexiós pontban maximuma van:

3. ábra. Az , ha x 0 és 0,3 közé esik	4. ábra. Az elsõ deriváltja

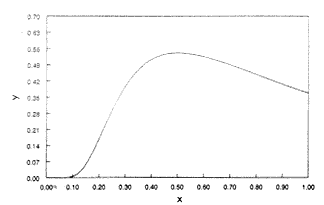
Ha y'-t ábrázoljuk x függvényében (4. ábra), látszik, hogy a deriváltnak 0,5 körül maximuma van. A második derivált megadja az inflexiós pont pontos helyét is:

Az 1 – 2x = 0 esetben x-re 0,5 adódik. Tehát az inflexiós pont x = 0,5-nél van (5. ábra).
 

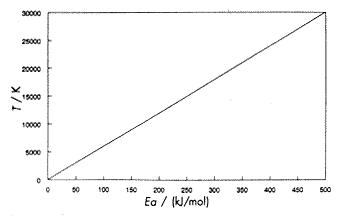
5. ábra. Az  második deriváltja	6. ábra Az inflexiós ponthoz tartozó hõmérséklet az aktiválási energia függvényéban

Térjünk most vissza az Arrhenius-egyenlethez és a kémiai kinetikához. Az egyszerûség kedvéért legyen E_a/R = a. A második derivált megadja az inflexiós pont pontos hõmérsékletét:

Az inflexiós pontot ismét úgy határozzuk meg, hogy az (a – 2T) kifejezést egyenlõvé tesszük 0-val, ekkor:

Ezt a függvényt ábrázolja a 6. ábra. A grafikon úgy értelmezhetõ, hogy bármely aktiválási energia esetén rendkívül nagy hõmérséklet szükséges ahhoz, hogy elérjük az Arrhenius-egyenlet nem "exponenciális" tartományát. Egy 200 kJ/mol aktiválási energiájú reakció esetén ez a hõmérséklet 12 000 K körül lenne, egy  60 kJ/mol aktiválási energiájú reakciónál 3600 K körül. A kémiai kinetikai vizsgálatok elég alacsony hõmérsékleten zajlanak ahhoz, hogy az Arrhenius-egyenlet mindig az "exponenciális emelkedõ" tartományban legyen.
 

---

Megjegyzés
1. Azért teszem idézõjelbe az "exponenciálisan növekvõ" kifejezést az  függvény vizsgálatakor, mert a függvény nem mutat valódi exponenciális növekedést. Ez csak az függvényre teljesül.