Ismeretes Löwdin [1] kérése, hogy indokoljuk a PSE periódusai betöltődésénél fellépő ismétlődéseket : 2, 8, 8, 18 , 18, 32, ... . Számos reagálás után Novaro [2] szerint "a PSE globális magyarázata" még nem lezárt. Ez a munka Löwdin kérésével kapcsolatban mond néhány szót.
Tekintsük az alábbi ábrát (1. ábra) :

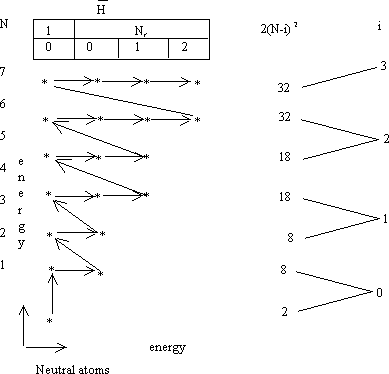
Az 1. ábra sokelektronos atomokban az atomi orbitálok betöltődési struktúráját mutatja be a jelen munka szerint. Ez lényegében a Meyer-Mendeleev táblázat. N a periódus-kvantumszám, l az azimutális kvantumszám, Nr a periódus radiális kvantumszám, 2(N-i)2 a periódusok betöltési száma, i az ismétlődési vagy kétperiódus kvantumszám, vagy a Coulomb-tér véletlen elfajulása és a periódusok véletlen elfajulása közti eltérés, vagy a hidrogén radiális kvantumszám és a periódus radiális kvantumszám közti különbség. A csillagok az Nl vagy Ns, NNr orbitálokat jelölik. (A periódusok orbitáljai nem Nl szerint rendeződnek.) A nyíl mutatja a betöltődés (elektronokkal a Pauli-elv szerint) sorrendjét. Ez megfelel a Bohr-féle Aufbau-elvnek vagy a Madelung-szabálynak, az energia növekvő sorrendjének és a periódusok növekvő Z sorrendjében töltődnek be. Ahhoz, hogy ez az ábra adódjon, bizonyos feltételeket kellett tenni. Megtartottuk a Schrödinger-egyenlet szögfüggő részét: érvényes a gömbszimmetria: lényegében multielektronos atomelméletről van szó centrális tér approximációban, amelyet a független részecske approximáció (IPA) egy-elektron atomelméletre egyszerűsít. A külső erőtér fix forrása a mag a KR origójában. A Schrödinger egyenletből indulunk ki, tehát nem veszünk figyelembe relativisztikus és kvantumelektrodinamikai effektusokat, csak az atomok multielektronos aspektusait tárgyaljuk. Ez egy effektív potenciál előírásával történik, amelytől megköveteljük, hogy az ábrán adott struktúrát szolgáltassa. Ezt csak úgy tudtuk elérni, hogy a Schrödinger-egyenletből kapott sajátértékek rendszerére bizonyos feltételt róttunk ki: ez a következő princípium: mivel a periódusok véletlen elfajulása majdnem megegyezik egy 3-dimenziós oszcillátor energianívóinak véletlen elfajulásával,
ezért azt követeltük,
hogy a  rendszert (PSE) olyan kvázioszcillátor
tér írja le, amelynek véletlen elfajulása
a periódusokéval azonos. Az elmélet tehát
ezen a két alapon (effektív potenciál és
kvázioszcillátor) nyugszik. Ez azt jelenti, hogy
a
rendszert (PSE) olyan kvázioszcillátor
tér írja le, amelynek véletlen elfajulása
a periódusokéval azonos. Az elmélet tehát
ezen a két alapon (effektív potenciál és
kvázioszcillátor) nyugszik. Ez azt jelenti, hogy
a  rendszer (PSE) Z=10-től elhagyja
a Coulomb-elfajulás elvét és egy 3-dimenziós
oszcillátor elfajulási elvét követi.
Szemléletesen: a neutrális atomban a mag és
a többi elektronok terében az elektronok töltéscsökkenést
(abszolút értékben) és azimutális
kvantumszám növekedést "éreznek".
Z=10-től kezdve a neutrális rendszer úgy
reagál ezekre a hatásokra, hogy lerögzíti
(fixálja) véletlen elfajulásainak számát,
azaz, a rendszer elkezdi felvenni egy 3-dimenziós oszcillátor
karakterét. Ez hozza létre az ismétlődéseket.
Z=10-től egy ilyen rendszerben a periódusokon belül
az orbitálok sorrendje képtelen követni a hidrogénszerű
sorrend elvét.
rendszer (PSE) Z=10-től elhagyja
a Coulomb-elfajulás elvét és egy 3-dimenziós
oszcillátor elfajulási elvét követi.
Szemléletesen: a neutrális atomban a mag és
a többi elektronok terében az elektronok töltéscsökkenést
(abszolút értékben) és azimutális
kvantumszám növekedést "éreznek".
Z=10-től kezdve a neutrális rendszer úgy
reagál ezekre a hatásokra, hogy lerögzíti
(fixálja) véletlen elfajulásainak számát,
azaz, a rendszer elkezdi felvenni egy 3-dimenziós oszcillátor
karakterét. Ez hozza létre az ismétlődéseket.
Z=10-től egy ilyen rendszerben a periódusokon belül
az orbitálok sorrendje képtelen követni a hidrogénszerű
sorrend elvét.
Összegezve: az ismétlődési
effektus a 3-dimenziós oszcillátor erők befolyása
az atomi héjakban. Ezek felelősek az irreverzibilis
konfigurációért ionizáció esetén:
az ionizált atomban az erős Coulomb-tér eltünteti
az ismétlődés (neutralitás) jeleit
és visszaállítja a Coulomb-sorrendet.
Hivatkozások:
[1] P.-O. Löwdin, Int. J. Quant. Chem. 3S, 331 (1969).
[2] O. Novaro, J. Mol. Struct.
(Theochem) 199, 103 (1989)