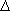 T = 0
T = 0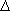 lnT = 0
lnT = 0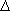 1/T = 0
1/T = 0
Stacionárius kvázilineáris hővezetésre lineáris esetben három differenciálegyenlet írható fel a három képi reprezentáció értelmében [1,2].
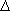 T = 0 T = 0 | 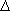 lnT = 0 lnT = 0 | 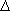 1/T = 0 1/T = 0 |
Azonban ez a Fourier képre vonatkoztatva csupán
mérnöki közelítésből fakad,
mert a Fourier törvénynek erre a lineáris 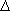 T = 0) esetre a természetben
nincs egzisztenciája. Így lineáris hővezetésre
csak két reprezentációs képben -energia
és entrópia képben- írhatók
fel a vonatkozó differenciálegyenletek a minimális
entrópiaprodukció elvének értelmében.
T = 0) esetre a természetben
nincs egzisztenciája. Így lineáris hővezetésre
csak két reprezentációs képben -energia
és entrópia képben- írhatók
fel a vonatkozó differenciálegyenletek a minimális
entrópiaprodukció elvének értelmében.
Kvázilineáris hővezetés esetére
összesen hat differenciálegyenlet írható
fel a fenti képi reprezentácóknak megfelelően,
azaz minden reprezentációs képben felírható
a másik két reprezentációs kép
kvázilineáris differenciálegyenlete direkt
variációval. Itt a minimumelvek [9,10] értelmében
szintén csupán két nemlineáris differenciálegyenlet
írható fel 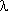 (T)
-re az energia valamint az entrópia képekben a direkt
variáció eredményeképpen.
(T)
-re az energia valamint az entrópia képekben a direkt
variáció eredményeképpen.
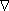 T)2 - L* T T)2 - L* T 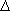 T = 0 T = 0 | 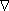 T)2 - L T T)2 - L T 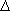 T = 0 T = 0 |
Az áramegyenlőség alapján felírható volt, hogy
L* = T 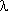 (T) (T)
| és | L = T2 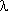 (T). (T).
|
A fennmaradó négy differenciálegyenlet mint megoldás csupán formális eredménynek tekinthető szempontunkból.
Egy dimenziós esetre Fourier képben az Euler-Lagrange
differenciálegyenletben a Lagrange sűrűségek
célszerű helyettesítésével (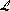 T,
T,
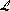 lnT,
lnT,
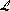 1/T)
kiterjeszthető a konkurrenciába vont függvények
száma s ez mint új tényező vehető
figyelembe a variációs probléma megoldásakor.
Általánosan az Euler-Lagrange differenciálegyenlet
megoldására és értelmezésére
a Gyarmati elvet használtuk kiegészítve az
említett új tényező elvével.
1/T)
kiterjeszthető a konkurrenciába vont függvények
száma s ez mint új tényező vehető
figyelembe a variációs probléma megoldásakor.
Általánosan az Euler-Lagrange differenciálegyenlet
megoldására és értelmezésére
a Gyarmati elvet használtuk kiegészítve az
említett új tényező elvével.
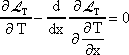
A Lagrange sűrűség Fourier képben a nemlineáris hővezetés egzisztenciáját mutatja stacionárius állapotban [8,14]. Nem igazolja azonban a lineárist.
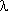 (T)
(T)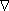 T
T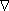 T =
T = 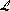 T(T)=
T2s
T(T)=
T2s
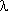 (T)
(T)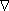 T
T
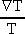 =
=
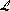 lnT=
Ts = L*
lnT=
Ts = L*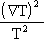
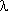 (T)
(T)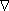 T
T
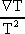 =
=
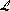 1/T=
s = L
1/T=
s = L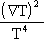
A differenciálegyenletekből 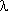 (T)-re
és
(T)-re
és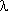 `(T)-re
(ahol
`(T)-re
(ahol 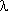 `(T)
=
`(T)
= 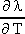 ) kapjuk,
hogy
) kapjuk,
hogy
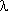 (T) =
(T) =
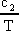 és
és
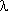 `(T) =
`(T) =
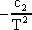 energiaképben,
és
energiaképben,
és
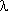 (T) =
(T) =
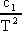 és
és
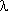 `(T) =
`(T) =
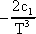 entrópiaképben.
entrópiaképben.
A konstansokra nézve c1 = T c2 kapcsolat lehetséges.
A 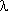 (T)
hővezetési tényezőre kapott kifejezés
egybeesik statisztikai mechanikában ismeretes eredménnyel,
az 1/T viszonynak megfelelően a magas hőmérsékletű
tartományban 100 K felett [3,4,5]
germániumra de sziliciumra is a mérésekkel
egyező az eredmény [11,12]. Az irodalomból
nyerhetően az állandó értéke
pl. germániumra kb. 20000 W/m.
(T)
hővezetési tényezőre kapott kifejezés
egybeesik statisztikai mechanikában ismeretes eredménnyel,
az 1/T viszonynak megfelelően a magas hőmérsékletű
tartományban 100 K felett [3,4,5]
germániumra de sziliciumra is a mérésekkel
egyező az eredmény [11,12]. Az irodalomból
nyerhetően az állandó értéke
pl. germániumra kb. 20000 W/m.
A stacionárius állapotbeli hőmérsékleteloszlást illetően tekintsünk egy egydimenziós hővezetési problémát, ahol a hő vezetése egy lemezen át történik. A lemez vastagsága l és a felületeket állandó hőmérsékleten tartjuk. A határfeltételek pedig T(x=0) = T0 és T(x=1) = T1 . A hőmérsékleteloszlások energia és entrópiaképekben az alábbiak:
T(x) = T0
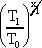 és
és
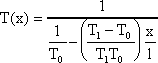 .
.
Emlékeztetőül a hőmérsékleteloszlás stacionárius állapotú hővezetés esetén állandó értékű fenomenológiai tényezővel, azaz Fourier típusú lineáris differenciálegyenletre, ami a formális lineáris megoldás:
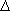 T = 0, T(x) = T0
+ (T1-T0)x/l .
T = 0, T(x) = T0
+ (T1-T0)x/l .
Ami az energiamérleg egyenletet illeti, látható a formális bizonyítás a lineáris esetre:
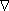 [
[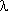
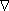 T] =
T] = 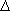 T
= 0,
T
= 0,
míg a kvázilineáris esetben a reális forma kapható meg a minimális entrópiaprodukció elvének megfelelően
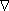 [
[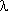 (T)
(T)
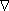 T] =
T] = 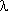 `(T)
(
`(T)
(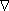 T)2 +
T)2 +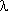 (T)
(T)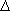 T
= 0.
T
= 0.
Így a minimumelvhez tartozó Euler-Lagrange differenciálegyenletek
teljesen egybeesnek az energiamérlegegyenlettel a kvázilineáris
tartományban. Látható, hogy a hővezetés
az irreverzibilis termodinamika elmélete szerint nemlineáris
folyamat a minimumelvekben rögzitett kényszerek és
az Onsager feltételek szerint. Mindemellett a mérnöki
gyakorlatban előforduló reális problémák
nemlineárisak [7,13]. Ez a helyzet tehát a Fourier
féle konstitutív egyenlettel, mert egy kísérleti
eredményt mindenkor teljes elméleti keretben kell
elhelyezni és értelmezni. A mérnöki
közelítés megengedhetőségének
mértékét ez határozza meg. Másrészről
állandó hővezetési tényező
esetén a variációs probléma [1,6]
azt eredményezi, hogy a konkurrenciába vont függvény
egyetlen és önmagával azonos, azaz a probléma
variációs természetű megoldásának
nincs egzisztenciája. Ez a minimumelvvel való értelmezést
kizárja, ami a fentiekben elmondottakkal teljes egyezést
eredményez.
Hivatkozások:
[1] Gyarmati, I., Springer, Berlin, Heidelberg, New-York (1970)
[2] Fekete, D., Phys. Stat. Sol. b 105, 161, (1981)
[3] Kreher, K., Reihe Mathematik und Physik. Akademie-Verlag, Berlin (1973)
[4] Linder, H., VEB Fachbuchverlag Leipzig (1978)
[5] Kittel, Ch., Introduction to Solid State Physics, 5th edition, John & Sons
[6] Biot, M. A., Oxford Press (1970)
[7] Kiss, E., Periodica Polytechnica, Ser. Chem. Eng., 38, 183, (1994)
[8] Kiss, E., Periodica Polytechnica, Ser. Chem. Eng. 41, 205, (1997)
[9] Lampinen, M. J., J. Non-Equilibrium Thermodynamics 15, 397, (1990)
[10] De Groot, S.R., Mazur, P., North- Holland Publishing Co., Amsterdam (1962)
[11] Glansdorff, P., Prigogine, I., Wiley Interscience (1971)
[12] Javorsky, B., Detlaf, A., Handbook of Physics. Mir Publishers, Moscow
[13] Cubo, R., Ichimura, H., Ushui, T., Hashitsume, N., Statistical Mechanics. Netsugaku - tokeingaku. The Shokabo and Company, Tokyo.
[14] Verhás, J., Atti Accademnia Peloritana dei Pericolanti, Messina, Italy, Sicily 62, 73, (1989)