A Természet Világa 1992. évi 3. számában megjelent cikk utóközlése
a folyóirat fôszerkesztôjének szíves engedélyével
|
A természet futball-labdái
Az elemi szén harmadik módosulata
Elgondolkodott-e már a kedves olvasó egy tangó típusú futball-labdát szemlélve azon, hogy vajon miért éppen egy ilyen, szabályos hatszögekbôl és ötszögekbôl álló testet használnak a gömb közelítéseként? Az utóbbi hónapokban komoly egyetemi tanszékeken és kutatóintézetekben tûntek fel labdával a kezükben sétáló, azt elmélyülten tanulmányozó kutatók. A hirtelen érdeklôdés oka, hogy nemrégiben a szénnek olyan módosulatát sikerült elôállítani, amely pontosan ilyen futball-labda alakú molekulákból áll.
Az elemi szén két kristályos módosulata a grafit és a gyémánt, ezek szerkezete látható az 1. ábrán.
A gyémántban a szén négy vegyértékének megfelelôen négy teljesen egyenrangú kötésben vesz részt minden szénatom. A réteges szerkezetû grafitban ezzel szemben valódi kémiai kötés csak a rétegeken belüli három szomszéddal alakul ki (ezért hasad a grafit olyan könnyen bizonyos síkok mentén), az elektronszerkezetet pedig úgy képzelhetjük el, hogy a szén négy vegyértékelektronjából egy "közös" lesz (delokalizálódik), mint a fémekben (ez a magyarázata a grafit elektromos vezetôképességének a síkok irányában).
A harmadik, a természetben elôforduló szénmódosulat, az amorf szén, köznapi nevén korom, amely fôként különbözô hosszúságú szénláncok rendezetlen keveréke.
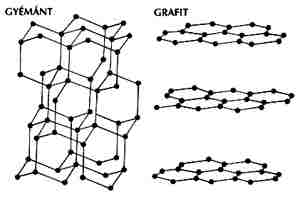 |
| 1. ábra. A szén két kristályos módosulata |
|---|
Zárt szerkezetû szénmolekula?
1984-ben, a korom tömegspektrumában észleltek elôször a 720-as tömegszámnál (tehát a 12-es tömegszámú szén hatvanszorosánál) éles csúcsot az Exxon kutatóintézetében (Linden, New Jersey, USA) Rohlfing és munkatársai. A rákövetkezô évben pedig egy houstoni (Texas, USA) és egy brightoni (Anglia) kutatócsoport közös erôfeszítésével, H. Kroto és R. Smalley vezetése alatt, sikerült olyan kísérleti körülményeket teremeteni, amelyek között a korom tömegspektruma már csak két csúcsot tartalmazott, 60 és 70 szénatomnak megfelelôen. Ez a tény igen stabil molekulákra utalt, hiszen a nagy vákuumban, nagy sebességgel száguldó részecskék általában hajlamosak arra, hogy egyes darabjaik leváljanak, széttöredezzenek és így általában számos, az anyamolekulánál kisebb tömegû fragmens jelentkezik a spektrumban. A kivételes stabilitás arra indította a kutatókat, hogy ne nyílt láncú, hanem valamilyen zárt szerkezetet tételezzenek fel, hasonlót a benzolhoz vagy az azzal rokon bonyolultabb vegyületekhez, amilyeneket a 2. ábrán mutatunk be. Az új lehetôség, ami felmerült, hogy vajon az ábrán látható síkbeli alakzatoktól eltérôen, létrejöhet-e háromdimenziós zárt szerkezet, tehát valamilyen poliéder.
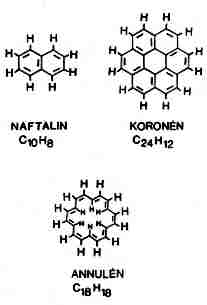 |
2. ábra. Zárt szerkezetû szénvegyületek:
kondenzált aromások (naftalin, koronén),
illetve a "belül üres" annuléncsalád
egyik képviselôje |
|---|
A kérdést, mint geometriai problémát, Euler már a 18. században megvizsgálta, és meg is fogalamzott egy feltételt arra nézve, hogy szabályos sokszög alakú lapokból mikor építhetô fel önmagába visszatérô zárt felület. Ez a feltétel a következô:
3n3 + 2n4 + 1n5 + 0n6 – 1n7 – 2n8 – 3n9 ... = 12
ahol n3, n4 ... a szabályos háromszögek, négyszögek stb. száma.
Alkalmazzuk ezt a feltételt a szénatom kémiájára! A szénvegyületekben a kötésszögeket a kapcsolódó atomok száma határozza meg, a rendszer mindig arra törekszik, hogy a kötések minél távolabb kerüljenek egymástól, mert az elektrosztatikus taszítás így lesz minimális. Négy szomszéd esetén az optimális kötésszög 109 fok (mint a tetraéderes elrendezésû gyémántban), három szomszédnál pedig 120 fok, mint a grafit hatszöges szerkezetében. Ha a szénatomok együttesét másmilyen szerkezetbe kényszerítjük, térbeli feszültséget okozunk, ami energianövekedéssel, azaz a stabilitás csökkenésével jár. Az energianövekedést a rendszer az elektronszerkezet szimmetriájának csökkenésével ellensúlyozhatja, így azonban csak néhány fokos szögeltérés kompenzálható. Az Euler-feltételnek eleget tevô, zárt felületû szénmódosulat a fentiek alapján tehát kizárólag szabályos ötszög (108 oC), illetve hatszög (120 oC) alakú lapokat tartalmazhat. Hogy hányat, azt azonnal megkapjuk a felírt egyenletbôl, ahol így n5 kivételével az összes együttható nulla lesz: n5 = 12, n6 pedig tetszôleges, hiszen már eredetileg is nulla volt a szorzója.
A footballeen labdába rúg
A tizenkét ötszögbôl és tetszôleges számú hatszögbôl felépített "lyukas molekula" ötletét D. E. H. Jones (aki a New Scientistben Daedelus álnéven írt rövid tudományos glosszákat) már 1966-ban felvetette. Hatvan szénatomot ilyen módon elrendezve, egy nagy szimmetriájú alakzat adódik, a csonkolt ikozaéder (3. ábra).
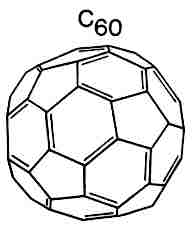 |
| 3. ábra. Buckminsterfullerén |
|---|
Sportkedvelôk azonnal felismerik a focilabdát, a felfedezôk viszont elôször egy amerikai építész, H. Buckminster Fuller által tervezett kupolás szerkezetre asszociáltak, innen ered az általuk adott név: buckminsterfullerene, ami azóta fullerénre, vagy egyszerûen "buckyball"-ra rövidült (a Chemical Abstracts ezzel szemben footballeen néven tartja nyilván). Saját bevallásuk szerint a gömbszerû molekula olyannyira tökéletesnek tûnt számukra, hogy elképzelhetetlennek tartottak bármiféle más geometriát – annak ellenére, hogy az anyagmennyiség semmilyen fizikai vizsgálathoz nem volt elegendô, és így a feltevést sem lehetett ellenôrizni. Lázas tevékenységbe kezdtek a kvantumkémikusok is, akik a fenti feltételeket egy újabbal – a zárt elektronhéj követelményével – kiegészítve, meg tudták állapítani azokat a bûvös szénatomszámokat, amelyekbôl hasonló molekulák keletkezhetnek: 24, 28, 32, 36, 50, 60 és 70. Néhányat a 4. ábrán mutatunk be. A 70 szénatomos csúcs a tömegspektrumban ezek szerint a C70 molekulának felel meg.
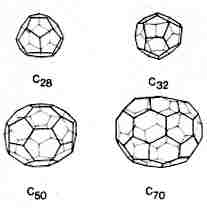 |
4. ábra. Lehetséges
fullerénszerkezetek |
|---|
Az a tény, hogy elôször a C60 és C70 molekulákat sikerült észlelni az ábrán láthatók közül, valószínûleg nem véletlen. A stabilitás ugyanis annál nagyobb, minél kevesebb közvetlenül érintkezô ötszög található benne (ezzel a kötésszögtorzulás csökken). Látható, hogy ez a két követelmény a C60-ban valósul meg a leginkább, de jó közelítéssel érvényes a C70-re is. A terület kísérleti vizsgálata a tavalyi év során kapta az elsô óriási lökést, amikor éppen ennek a két anyagnak nagy tömegben (néhány gramm/nap) való elôállítására dolgoztak ki módszert Krätschmer és társai, egy heidelbergi és egy tucsoni (Arizona, USA) kutatócsoport tagjai. Addigra már az összes, kvantumkémiai módszerekkel megjósolható tulajdonságok (az elektrongerjesztési energiák és a rezgési frekvenciák) ki voltak számolva. A modern kvantumkémiai módszerekkel ugyanis a viszonylag kevés elektront tartalmazó szénatomkból felépített rendszerek jól kezelhetôk, ugyanakkor a szokatlan geometria kihívást is jelentett, új számítási eljárások kidolgozására kínált lehetôséget. Ezek sikerét jelezte, valamint az eredetileg csak sejtett szerkezetet igazolta, hogy miután lehetôvé vált a C60 és C70 spektroszkópiai vizsgálata, az eredmények igen jó egyezést mutattak a több évvel korábbi számolásokkal. A röntgendiffrakciós vizsgálatok is alátámasztották a gömbszerû alakzatokból felépülô kristályszerkezetet.
A C–60 szintézise
Ez az újfajta szénmódosulat elsô ránézésre megválaszolandó kérdések és a szintetikus lehetôségek sokaságát veti fel a kémia bármely területén dolgozó kutatók számára. Az elsô kérdés a kötések jellege, azaz hogy a 3. ábrán berajzolt, váltakozó egyes, illetve kettôs kötések mennyire felelnek meg a valóságnak. A magmágneses rezonanciaspektrumban, amely nagyon érzékeny a kémiai környezetre, Taylor és munkatársai csupán egyetlen csúcsot észleltek, bizonyítva, hogy a C60 molekula minden szénatomja ekvivalens. Ez megvalósulhat az ábrán feltüntetett módon úgy, hogy az ötszögek oldalait egyes kötések, a hatszögekéit pedig váltakozó egyes-kettôs kötések alkotják.
A másik véglet a benzolhoz hasonló elektronelrendezés lenne, ahol minden kötés egyforma, és szénatomonként egy elektron a teljes felületen egyenletesen oszlik el, delokalizálódik. Nem világos azonban, hogy az aromás jelleg fogalma görbült felületre egyáltalán alkalmazható-e. Kötéshossz-számolások a váltakozó modellt valószínûsítik, és erre utal Hauflernek és társainak egy szintetikus tapasztalata is. A C60 ugyanis a Birch-redukcióval (lítiummal folyékony ammóniában) C60H36-tá hidrogénezhetô. Ez a reakció általában aromás vegyületekkel nem játszódik le. Hidrogénen kívül már metilcsoportokat is sikerült a gömbök külsejére "akasztani", és ezzel egy egészen újfajta kémia távlata merül fel, hiszen az oldalláncok módosításával a variációk szinte kimeríthetetlenek. További lehetôség egyéb atomok bevitele a labda belsejébe, tömegspektrometriás bizonyíték már erre is van: számos fémmel sikerült ilyen komplex molekulákat produkálni.
A C60-ban dús korom elôállításának fent említett technológiája egyébként nem túlságosan bonyolult, egy ívfényes párologtató berendezés kis módosításával megvalósítható; a koromból pedig közönséges tisztító eljárásokkal (extrakció, illetve oszlopkromatográfia) ki lehet nyerni a 99%-ban tiszta C60-at. Az a sebesség, amellyel a világban a "füstölés" elterjedt, csak a réz-oxid alapú szupravezetôk öt évvel ezelôtti hódításához mérhetô – de ebben nem merül ki a hasonlóság. A fizikusok ugyanis általában nem lelkesednek az aromás jelleg vagy a gömbbe zárt fématomok rejtelmei iránt: az ô érdeklôdésük felkeltéséhez egy további szenzáció kellett, mégpedig az, hogy a C60 alkálifémekkel képzett sói szupravezetést mutatnak, a káliumsó 18, a rubídiumsó pedig 30 Kelvin-fok alatt vezeti ellenállás nélkül az elektromos áramot. (Itt az alkáliionok nem a gömbök belsejébe, hanem a kristályrácsban a gömbök között létrejövô hézagokba épülnek be.) Ezek a hômérsékletek alacsonynak tûnhetnek a rézvegyületekben elért 120 K-hez képest, de arra még sokan emlékeznek, hogy ott is egy 36 kelvinen szupravezetô anyag indította el a lavinát... Külön öröm, hogy ebben a munkában két honfitársunk is komolyan "labdába rúgott": Holczer Károly, a University of California, Los Angeles vendégprofesszora a rubídiumvegyület szupravezetésének felfedezésében, Mihály László, a Stony Brook-i New York Állami Egyetem professzora pedig a kristályszerkezet meghatározásában.
A lehetséges alkalmazások ennél jóval szélesebb körûek: a fullerén szóba jöhet mint kenôanyag, a fémkomplexképzési hajlam beláthatatlan lehetôségeket biztosít a katalízisben, a szinte határtalan módosítási lehetôség pedig olyan reagensek elôállításával kecsegtet, amelyek – bátran mondhatjuk – forradalmasíthatják a szerves kémiát.
Füstölô csillagok
Elôfordulhatnak-e fullerének a természetben? Kis mennyiségben a közönséges koromban szinte biztosan, de van egy ennél sokkal izgalmasabb lelôhely is: a csillagközi tér. Szénben gazdag csillagok folyamatosan eregetnek füstöt magukból, és ezt a csillagászok spektroszkópiai módszerekkel már régen tanulmányozták. A mért spektrumokban van jó néhány vonal, az ún. diffúz csillagközi sávok, amelyeket eddig nem sikerült semmilyen ismert anyaghoz rendelni. A C60 izolálása után felmerült a remény, hogy legalább néhány ilyen sávra magyarázatot találnak, de a C60-gôz infravörös emisszióját összehasonlítva a csillagközi spektrumokkal, Frum és munkatársai nem találtak egyezést. Ennek egyik lehetséges oka, hogy – mint Taylor és társai megmutatták – a molekula ultraibolya fény hatására elbomlik, az pedig csillagok környékén bôven van. Stabilnak találták viszont a molekulából képzett pozitív iont, továbbá a hidrogénezett származékokat. Ezek spektruma ma még nem ismert, de várható, hogy elôállításuk és vizsgálatuk – éppen, mert errôl az oldalról is igény van rá – a közeljövôben megtörténik. A hidrogénezett származékok minden valószínûség szerint reakcióképesebbek, mint az alapmolekula, tehát újabb kémiai folyamatokra (pl. nitrogénnel) van lehetôség. Ez messze vezetô spekulációkat indíthat el, akár az élet keletkezésével kapcsolatban is.
Rövid távon a haszon mindenképpen az, hogy intenzív párbeszéd indul meg a természettudomány különbözô területeit mûvelôk között, és ennek során szerves vegyészek, kvantumkémikusok, szilárdtestfizikusok, csillagászok, biológusok mind nagyon sokat tanulhatnak egymástól. Talán ez a legszebb a természettudományos alapkutatásban.




