A termodinamika második fôtétele
A makroszkopikus termodinamikában ismét CLAUSIUS jut szóhoz. Elfogadva a hô és mechanikai munka ekvivalenciáját, vagy általánosabban, az energiamegmaradás elvét, észreveszi, hogy a termodinamikai jelenségek magyarázatához még egy új elvet is meg kell fogalmazni. CLAUSIUS (1854) kiindulásul azt az axiómát fogadja el, hogy hô magától nem áramlik hidegebb testrôl melegebbre. Ez az axióma a termodinamika második fôtételének egyik közérthetô megfogalmazása. Egy másik – ezzel egyenértékû – axióma: nem lehetséges másodfajú perpetuum mobilét konstruálni – egyszerûen szólva olyan berendezést, amely az energia megmaradási tételének ugyan nem mondana ellen, de a hôt 100%-os hatásfokkal alakítaná mechanikai munkává.
...
A kémikus WALTHER NERNST (1864–1941), valamint MAX PLANCK vizsgálatai 1904-ben ill. 1911-ben vezettek el a termodinamika harmadik fôtételéhez:
3. Minden termikus egyensúlyban levô test entrópiája nullához tart, ha az abszolút nulla hômérséklethez tartunk.
A fenomenologikus termodinamika továbbfejlesztése, heterogén rendszerekre való kiterjesztése elsôsorban HELMHOLTZ és GIBBS érdeme a XIX. század nyolcvanas éveiben. A XX. században az érdeklôdés eltolódott a nem egyensúlyi állapotok és irreverzibilis folyamatok irányába – különös hangsúlyt fektetve a biológiai jelenségekre (PRIGOGINE, ONSAGER, GYARMATI).
Az entrópia elsô pillanatra igen elvont fogalomnak tûnhet, amelynek csak az elméleti fizikában van helye. Gyakorlati jelentôséget ad azonban az a tény, hogy ugyanolyan állapotjellemzôként használható, mint a nyomás, térfogat vagy hômérséklet. Ma már a mindennapi mérnöki gyakorlatban, gôzgépek méretezésénél például, kiterjedten alkalmazzák a T–S (hômérséklet-entrópia) diagramokat.
Szerepét a mindennapi élet számára is lehet érzékeltetni: olyan egyszerû törvényszerûségek kvantitatív leírását segíti elô, mint amilyen az például, hogy egy lezárt rendszerben a különbözô hômérsékleten levô testek elôbb-utóbb közös hômérsékletet vesznek fel.
Ez utóbbi megállapítást vetítették ki az egész világegyetemre az úgynevezett "hôhalál" elméletben. Ezek szerint a világegyetem jelen pillanatban alacsony entrópiájú állapotban van – ami azt jelenti, hogy igen különbözô hômérsékletû testeket találunk benne. Minthogy a világban végbemenô minden történés a világegyetem összentrópiájának növelését eredményezi, így végül is világunk eljut a maximális entrópiájú állapotba: ekkorra már minden hômérséklet-különbség kiegyenlítôdött, és ezzel megszûnik minden élet lehetôsége is. Ez a következtetés fizikai szempontból nézve két okból sem helytálló. Az egyik: a törvény véges lezárt rendszerre vonatkozik; a másik pedig: a második fôtétel valószínûségi törvény, tehát a jelenségek lefolyásának Iegvalószínûbb menetét adja, amelytôl, ha csak kis valószínûséggel is, de eltérések lehetségesek.
KELVIN hangsúlyozta elôször 1852-ben, hogy a természeti
folyamatokban olyan tendencia nyilvánul meg, hogy a különbözô
energiafajták végül is hôenergiává
alakuljanak, kiegyenlítve minden hômérsékletkülönbséget.
SCHOPENHAUER ez idô tájt divatba jövô pesszimizmusa
filozófiai hátteret is biztosított a tudomány
eme legfrissebb eredményeinek. Különösen CAMILLE
FLAMMARION (1842–1925) francia csillagász széles körben
elterjedt, népszerû, hatásos illusztrációkkal
ellátott könyveiben festette le Földünk pusztulását
nagy meggyôzô erôvel. Az ember tragédiájának
falanszterjelenete sejteti velünk a ránk váró
végzetet, amely az eszkimó jelenetben a maga realitásában
elénk is tárul.
Entrópia és valószínûség
A hatvanas évek közepe táján már lerögzítôdött a makroszkopikus (fenomenologikus) termodinamika két fôtétele, a kinetikus gázelmélet pedig sikeresen birkózott meg az állapotegyenlet értelmezése után a hôvezetés és a viszkozitás magyarázatával is (MAXWELL: On the Dynamical Theory of Gases, 1866–1868; ezekben a cikkekben szerepel egyébként a sebességeloszlás-függvény új, egzaktabb levezetése is).
A gáz állapotegyenlete, sôt az elsô fôtétel egyszerû mechanikai elvek (impulzus-tétel, energia megmaradás) segítségével értelmezhetôvé vált, így nem csoda, ha azonnal felmerült az igény a második fôtétel gázkinetikai értelmezésére. A második fôtétel matematikai megfogalmazásában az entrópia játssza a fôszerepet, így a legelsô kísérletek arra irányultak, hogy kizárólag a mechanika törvényeit használva bizonyítsák be – megfordítható folyamatokat vizsgálva – hogy a dS = dQ/T kifejezés teljes differenciál, más szóval létezik az entrópia mint állapotjelzô (RANKINE 1865, BOLTZMANN 1866, CLAUSIUS 1871). A legkisebb hatás elvének egy általánosabb megfogalmazásából indultak ki, de a kitûzött cél elérésére kezdetben az egyes atomok mozgására igen erôltetett feltevéseket kellett tenni; így például azt, hogy mindegyik atom zárt pályán mozog azonos periódusidôvel. Bár a megszorításokat idôvel sikerült lazítani, a hetvenes évek elejére kiderült, hogy a második fôtétel értelmezése – különösen irreverzibilis folyamatok esetében – tisztán mechanikai elvek segítségével nem lehetséges.
...
Vizsgáljunk egy N molekulából álló rendszert. A molekulák szerkezete akármilyen bonyolult lehet. Ilyen módon egy-egy molekula állapotának megadásához is több adatra van szükségünk.
Nevezzük az f szabadságfokkal bíró molekula helyzetét egyértelmûen megadó f számú koordinátát rendre q1, q2 ... qf-nek. Amikor egy molekulán megfigyelést végzünk, állapotát nem az x, y, z koordinátákkal jellemzett térben, hanem a q1, q2 ... qf koordináták f dimenziójú terében megadott ponttal jellemezhetjük.
A molekula állapotának teljes jellemzésére helyzetén kívül mozgási állapotát is ismernünk kell. Ezt legcélszerûbben a p1, p2 ... pf impulzus megadásával érjük el. Itt természetesen a q1, q2 ... qf "helykoordináták"-hoz tartozó "kanonikusan konjugált" impulzusokról van szó: ezek azok a q és p mennyiségek, amelyek a Hamilton-mozgásegyenletben is szerepelnek.
Egy molekula helyzetét és mozgását, vagyis mozgásállapotát így a 2f darab q1, q2 ... qf; p1, p2 ... pf koordináta határozza meg. Képzeljük el ezeket, mint egy 2f dimenziós tér közönséges Descartes-koordinátáit. Tehát az elsô tengelyre q1-et, a másodikra q2-t, ... a 2f-edikre pedig pf-t vigyük fel. Ne zavarjon az bennünket, hogy szemléletesen csak q3-ig tudjuk eljárásunkat követni, mert mindez csak egyszerûsítô beszédmód. Az így kapott teret a molekula fázisterének nevezzük. Most már azt mondhatjuk, hogy a molekula teljes állapotát a fázistér egy pontja jellemzi. Ebben ugyanis mind a hely, mind az impulzus koordinátái benne vannak. Most a fázisteret osszuk fel dq1 ... dqfdp1 ... pf köbtartalommal bíró térfogatelemekre és számozzuk meg az így elôálló egyes "cellákat". Ezzel a számozással jellemeztük a fázistér egyes helyeit. A gáz állapotát minden részletében ismerjük, ha megmondjuk egy adott pillanatban minden egyes megjelölt "individualizált" molekuláról, hogy a fázistér melyik cellájában tartózkodik. Ezzel ugyanis mind a helyzetét, mind a sebességállapotát megadtuk mindegyik molekulának. A gáznak egy ilyen, minden egyes individualizált molekula összes koordinátáinak megadásával jellemzett állapotát mikroállapotnak hívjuk. A kiindulási valószínûségünk: a gáznak minden, a fentiek szerint meghatározott mikroállapota egyformán valószínû.
A gáznak a mérések számára hozzáférhetô makroállapotát az egyes cellákban helyet foglaló molekulák száma, vagyis a molekulák fázistérbeni sûrûsége határozza meg.
A fázistér egyes celláiban N1,
N2
... Nn molekulát elhelyezve, az N1,
N2
... Nn számokkal jellemzett makroállapotot
kapjuk. Az ezt megvalósító mikroállapotok száma
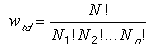 |
(1) |
Ezt a kifejezést nevezzük ezen állapot termodinamikai valószínûségének.
Egy tetszôleges kiindulási helyzetben levô gázt magára hagyva rövidesen átmegy olyan állapotba, amelyben a gáz termodinamikai valószínûsége maximális. Így például ha egy edény fallal elválasztott két részében különbözô nyomású gáz van, akkor együtt tekintve a két térfogatot, ennek az eloszlásnak a valószínûsége sokkal kisebb, mint az egyenletes eloszlásé. Megszüntetve tehát az elválasztófalat, a sûrûségkülönbség kiegyenlítôdik. Vagy: homogén egyenletes sebességû gázsugarat juttatva egy edényben levô gázba, molekuláinak sebessége rövidesen megváltozik: egyenletesen szétszóródnak minden irányban, sebességük abszolút értéke pedig a Maxwell-eloszlást követi, minthogy ez sokkal valószínûbb, mint a kiindulási állapot.
Az (1) kifejezés maximális értékét az N1= N2 = N3 = ... esetben, vagyis állandó sûrûségnél veszi fel, feltételezve, hogy ugyanaz az energiaérték tartozik a fázistér minden egyes térfogatelelméhez. Tartozzék azonban az Ei energia azon térfogatelemhez, amelybe Ni részecske tartozik és legyen az egész rendszer összenergiája E0 adott, akkor az (1) kifejezés maximális értékét azon N1, N2 ... Ni, ... eloszlások között kell megkeresnünk, amelyekre nézve az E0 = SiNiEi egyenlet érvényes. A matematika nyelvén szólva ilyenkor kötött szélsô értéket kell keresnünk. A legnagyobb valószínûséget adó eloszlás:
Ez a Boltzmann-féle eloszlásfüggvény.
Ezzel egyúttal a termodinamikai valószínûségben egy, a jelenségek lefolyásának irányát mutató mennyiséget találunk: a természetben a jelenségek úgy folynak le, hogy közben a részt vevô testek együttes termodinamikai valószínûsége növekszik. Ez a mondat ismerôsen hangzik: az elôzôekben ugyanis ugyanezt mondtuk az entrópiáról. Az entrópia az a mennyiség, amely a makroszkopikus termodinamikai jelenségeknél megszabja a jelenségek lefolyásának irányát. A második fôtétel szerint ugyanis minden valóságos folyamatnál az entrópia nô. Tehát egy adott eloszlású gáz termodinamikai valószínûsége és entrópiája között szoros összefüggésnek kell lennie. Az entrópia valamilyen függvénye a valószínûségnek.
Ezt a függvényt könnyen meg is tudjuk állapítani.
Két, egymás mellett levô, egymástól független
gáz együttes entrópiája ugyanis a termodinamika
szerint a két gáz entrópiájának összege:
S1
+ S2 = S. Viszont annak valószínûsége,
hogy a két gázt egy idôben találjuk a megadott
állapotban, W=W1W2, ha
W1
az egyik, W2 a másik gáz termodinamikai
valószínûsége. Tudjuk ugyanis, hogy két
független esemény egyszerre való bekövetkezésének
valószínûsége egyenlô az egyes események
valószínûségének szorzatával.
Ebbôl következik, hogy az S=f(W)-nek olyannak
kell lennie, hogy az S1 + S2 = S
egyenletnek megfelelôen f(W1 + W2)=f
(W1)f(W2).
Ez az összefüggés
már meg is határozza az f (W) függvényt:
S=k ln W,
ahol k univerzális állandó; a szorzat logaritmusa
ugyanis valóban egyenlô a tényezôk logaritmusának
összegével. Ezt a kapcsolatot BOLTZMANN
1877-ben írta fel, MAXWELL pedig 1879-ben általánosította.