
Copyright David G. Green 1993. Revised 1995. This preprint may be copied and used provided that this notice and the authorship details remain attached.

Az alábbi cikk angol nyelvû eredetije itt található.
Milyen hosszú Nagy Britannia partvonala? Elsô pillantásra ez a kérdés triviálisnak tûnik. Egy térkép és egy vonalzó segítségével bárki rövid idôn belül meg tudná mondani az eredményt. A gond csak az, hogy egy nagyobb léptékû térképpel megismételve a mérést, az elôzônél nagyobb eredményt kapnánk (1. ábra). Ha ténylegesen lemennénk a partra és ott végeznénk el a mérést, akkor egy még nagyobb értéket kapnánk. Kiderül, hogy minél kisebb skálán végezzük a mérést, annál nagyobb eredményt kapunk, és ennek a növekedésnek nem lesz határa. Így, ha az (elméleti) mérésnél a felbontás végtelen kicsi lenne, akkor a becsült hossz végtelen naggyá válna. Ezt az összefüggést a mért hosszúság és a felbontás között elsôként Lewis Fry Richardson vette elôször észre (ld. Mandelbrot, 1993).
Ha a mérésekrôl beszélünk, akkor a felbontás jellemezhetô meghatározott hosszúságú mérôrudakkal: minél finomabb a felbontás, annál rövidebb a rúd. Így a görbét úgy is tekinthetjük, mintha egymáshoz csatolt, azonos hosszúságú rudakból állana (1. ábra). Világos, hogy az így kapott képen nem látszanak azok a részletek, amelyek kisebbek, mint a rudak. Természetesen senki sem úgy készíti a térképet, hogy ténylegesen rudakat fektet a talajra, de ez az analógia jól leírja azt a problémát, amit a légifotók véges felbontása, a felszíni mérôpontok távolsága vagy a rajzolásnál használt toll vastagsága okoz. Ugyancsak hasonló a probléma a biológiai mérések pontosságánál vagy a mintavételi gyakoriságánál.
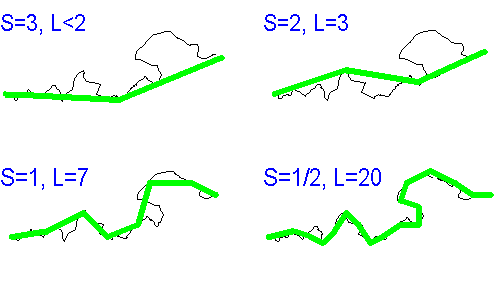
1. ábra: A partvonal L hosszának becslése S hosszúságú mérôrudakkal.
A hossz- (illetve a terület-)függés komoly problémát okoz a biológusoknak. Például a nagyon szabálytalan partvonalú tavaknál a sekély vizek aránya nagy a teljes vízfelszínhez képest. és így gazdagabb az állat és növényviláguk , mint a szabályos partvonalúaké. A különbözô felbontások miatt igen nehéz olyan jellemzést találni a partvonalak élôvilágának leírására, amelyben a teljes vízfelszínt és a partvonal hosszát használják fel.

2. ábra: Keresztrajzolás egyszerû iterációval.
A különbözô felbontások által okozott problémák leírására javasolta Mandelbrot a fraktálok használatát. Az ô meghatározása szerint a minden olyan görbe vagy felszín fraktál, amely a felbontástól független. Ez a tulajdonság (az önhasonlóság) azt jelenti, hogy a görbe bármely részét felnagyítva az eredetivel azonos görbét kapunk vissza. Így az egyik felbontásról a másikra való átmenetelt egy iterációs eljárással is jellemezhetjük (pl. ld. a 2. ábrát).
Egy igen fontos különbség a fraktál görbék és a természetben elôforduló görbék között az, hogy a fraktálok sehol sem differenciálhatók. Ennek oka az, hogy bár a fraktálok folytonosak, de mindenütt hoporcsosak. A fraktálokat úgy írhatjuk le, hogy megvizsgáljuk, hogyan változnak különbözô felbontásoknál.
A fraktáldimenzió segítségével meghatározható, mennyire szabálytalan egy fraktál görbe. Általában a vonalakat egydimenziósnak, a felületeket kétdimenziósnak, a testeket pedig háromdimenziósnak tartjuk. Azonban egy nagyon szabálytalan görbe ide-oda vándorolhat a felületen, olyannyira, hogy szinte teljesen ki is töltheti azt. Nagyon tekervényes felületek, mint pl. egy fa lombozata, vagy a tüdô belsô felülete majdhogynem háromdimenziósak. Így a szabálytalanságra, hepehupásságra úgy tekinthetünk, mint a dimenzió növelésére: egy szabálytalan görbe dimenziója 1 és 2 között lesz, míg egy szabálytalan felületé 2 és 3 közé esik. Egy fraktálgörbe dimenziója egy olyan szám, amely azt jellemzi, hogy a görbe két kiválasztott pontja között hogy nô a távolság, midôn növeljük a felbontást. Tehát amíg a vonal és a felület topológiai dimenziója mindig 1, illetve 2, addig a fraktáldimenzió lehet egy ezek közti érték is . A D fraktáldimenzió definíciója
log (L2/L1)
D= -------------- ... (1)
log (S1/S2)
ahol L1, L2 a görbén mért hosszúságok, S1 és S2 pedig a használt mérték nagysága (azaz a felbontás).
Az 1. ábrán látható partvonalnál S=1, ill. S=1/2 esetben L=7, ill. L=20. Így
D= log(20/7)/log(2)=1.51
Ugyanígy, ha S=1-rôl S=2-re térünk, egy másik, kissé alacsonyabb fraktáldimenziót kapunk (D=1.22), míg S=2-rôl S=3-ra térve D körülbelül 1.13 lesz.
Fontos tisztában lennünk azzal, hogy a fraktáldimenzió fentebb bemutatott becslése csak bizonyos fajta adatoknál használható. Tegyük fel, hogy pl. egy korallzátony felületét akarjuk megmérni. Két különbözô módszert használhatunk. Elsôként elkezdhetjük mérni a távolságot a zátony két pontja között, úgy, hogy közben változtatgatjuk a felbontást. Ekkor a fraktáldimenziót az 1. egyenlet segítségével számolhatjuk ki. Azonban hogyha például a zátony egy metszetét vizsgáljuk, és a zátony magasságát mérjük a talapzathoz képest a metszet mentén, akkor a fraktáldimenziót már nem számíthatjuk ki az elôzô módszerrel. A magasságadatok segítségével a fraktáldimenzió a spektrum vagy variogram segítségével állapítható meg. Kiderül, hogyha D a fraktáldimenzió, w a frekvencia, és S(w) w spektruma, akkor
S(w) ~ k w^5 - 2D ... (2)
Azzal is tisztában kell lennünk, hogy az igazi fraktál csak egy idealizáció. A valós világban elôforduló görbék, illetve felületek nem valódi fraktálok; olyan folyamatok hozták létre ôket, amelyek csak egy meghatározott mérettartományban fekvô alakzatokat képesek kialakítani. Így D változhat a felbontással, mint azt a fenti ábrán is láttuk. A változás segíthet abban, hogy jellemezhessük a létrehozásban közremûködô folyamatokat. Mandelbrot ezeket a különbözô keltési folyamatokhoz tartozó mérettartományokban jelentkezô töréseket átmeneti zónáknak nevezte.
Az önhasonlóság azt jelenti, hogyha egy fraktált kicsinyítünk vagy nagyítunk, a kinézete ettôl nem változik. Ebbôl az következik, hogy a fraktálok általában úgy alakulnak ki, hogy egy egyszerû mintázat állandóan ismétlôdik kisebb és kisebb mérettartományokban (ld. pl. a 2. ábrát). A fraktálokat létrehozó eljárások egyik fontos csoportja az ú.n. véletlen iterációs algoritmusok. Ezek az eljárások ahhoz hasonlítanak, amikor véletlenszerûen bepöttyözzük a papírt egy tollal. Azonban ahelyett, hogy a tollat teljesen összevissza mozgatnánk, a mozgást bizonyos elôre meghatározott szabályok irányítják; minden alkalommal ezek közül a szabályok közül választunk ki véletlenszerûen egyet (minden szabályhoz meghatározott kiválasztási valószínûség tartozik), és az adott lépésben a kiválasztott szabály irányítja a tollat. Ezeket a szabályokat ú.n. affin transzformációkkal definiálhatjuk. Egy két dimenziós A affin transzformáció nem más, mint egy olyan függvény, amiben a mérteváltoztatások, eltolások és forgatások szerepelnek. Az általános alakja a következô:
Ax(x) = ax + by + e ...(3) Ay(y) = cx + dy + f
![]()
Az 1. táblázatban a páfrányhoz és fûhöz hasonló képek készítéséhez használt algoritmus transzformációihoz való információk találhatók. A táblázatban megtalálható minden transzformációhoz a szükséges a, b, c, d, e és f paraméter. A p valószínûség azt határozza meg, milyen gyakran használandó az adott transzformáció.
3. ábra: Egy fraktális páfrány.
1. táblázat: Néhány egyszerû fraktál affin transzformációi
* Ld. a 3. egyenletet.
A Brown-mozgás a 2 dimenziós fraktált elôállító eljárások egyik példája. Mikroszkopikus részecskéknél fordul elô a vízmolekulák lökdösôdésének eredményeképp (amennyiben vizes a közeg). Az ilyen részecskék pályája egy olyan "véletlen bolyongás", amikor mind az irány, mind a távolság egyenletes eloszlású véletlenszerû változó. Azaz a ha a részecske a sík egyik meghatározott pontjából a másikba akar jutni, akkor a pályája szinte biztos, hogy kitölti az egész síkot, mielôtt célba érne.

A Brown-mozgás hatása a kristályok növekedésénél is megfigyelhetô. A 4. ábrán látható, hogy milyen alakzatok alakulnak ki lehulló részecskékbôl, ha az oldalirányú sebesség (h), illetve a megtapadási valószínûség (p) változik. Az ábrák a következô értékeknek felelnek meg: (a) h=1, p=0; (b) h=1, p=1; (c) h=10, p=0; (d) h=10, p=1. A megtapadt részecskék (ennek az ábrán a p=1 felel meg) fa-, illetve mohaszerû alakzatot hoznak létre. Ezt a tulajdonságot fel is használják rajzfilmeknél a növények, illetve a tájkép megrajzolásához.
4. ábra: Zuhanó részecskék Brown-mozgásából létrejövô alakzatok.
A tüdônek az a képessége, hogy mennyi oxigént tud felvenni a belélegzett levegôbôl, arányos a rendelkezésre álló felülettôl. Azaz egy adott tüdôtérfogat esetén igen jó, ha a felszínt megnöveljük. A tüdô szöveteinek belsô felülete ezért igen magas fraktáldimenziójú.
További, a fraktálokkal kapcsolatos információk találhatók Mandelbrotnál (1975) és Barnsley-nél (1988).
Ugyancsak nézzük meg az NCSA The Fractal Microscope (A fraktálmikroszkóp) címû on-line bemutatóját, valamint az ugyanott levô Fraktálgeometria és Irodalomjegyzék részeket.
Egy alakzat fraktáldimenzióját kiszámolhatjuk a fractop szolgáltatás igénybe vételével. Ehhez Netscape v.2-re, vagy más, olyan böngészôre van szükség, amivel fájlokat küldhetünk más WWW-szerverre.
A fraktálokról és más hasonló dolgokról találhatunk információkat a Complex Systems Network-ön. További on-line információkhoz kereshetünk ugrópontokat a Complex Systems Virtual Library-ban.
1. Használjuk a FRACTINT programot fraktálok rajzolásához.
(a) Vessünk egy pillantást a Mandelbrot-halmazra (ez tûnik fel a program indításakor). Vizsgáljuk meg az alakzat keskeny "parti sávját", ami a középsô régiót a sík külsô részeitôl elválassza.
(b) Próbáljunk meg találni egy olyan részt, amely úgy néz ki, mint maga a teljes halmaz. Használjuk a nagyítás (zoom) lehetôségét, és nézzük meg jobban ezt a részt. Még mindig emlékeztet a teljes halmazra? Találunk-e még kisebb részeket, amik szintén emlékeztetnek az eredetire?
2. Válasszuk az IFS opciót. Nézzünk meg néhány ábrát (pl. a páfrányt).
Copyright David E. Green,
Environmental and Information Sciences, Charles Sturt University