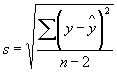 (7.17)
(7.17)
Tételezzük fel, hogy az y mennyiség valóban lineáris függvénye x független változónak. Ebben az esetben csak a mérési hiba az oka annak, hogy a mért pontok nem esnek pontosan a becsült egyenesre. Ebbõl következik, hogy ebben az esetben az
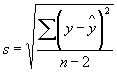 (7.17)
(7.17)
mennyiség a mérési hiba becslése. (A szabadsági fok azért n - 2, mert az egyenes két állandója két megkötést jelent az y mért értékek között). Ez a becslés egyébként
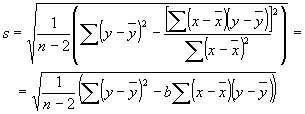 (7.18)
(7.18)
módon is számítható.
Felvetõdik ezekután a paraméterek és
a kapott paraméterekkel
számitott ![]() értékek
szórásának becslése. Ezek rendre a következõk:
értékek
szórásának becslése. Ezek rendre a következõk:
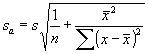 (7.19)
(7.19)
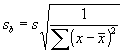 (7.20)
(7.20)
Normális eloszlású y értékek esetén adott valószínûségû konfidencia tartományt is megadhatunk a paraméterekhez.
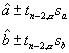 (7.21)
(7.21)
A becsült paraméterekkel bármely x* változóhoz
kiszámítható egy ![]() érték
várható értékének szórása:
érték
várható értékének szórása:
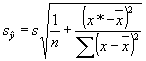 (7.22)
(7.22)
Ez az x*-tól függõ mennyiség a regressziós
egyenes felett és alatt megadja a konfidencia "övet", tájékoztat
arról, milyen határok között mozog a regressziós
egyenes 1 - a valószínûséggel.(7.1 ábra).
Mint látható, a konfidencia tartomány az egyenes "súlypontjában"
(az![]() pontban) legkeskenyebb
és az egyenes két széle felé nõ.
pontban) legkeskenyebb
és az egyenes két széle felé nõ.
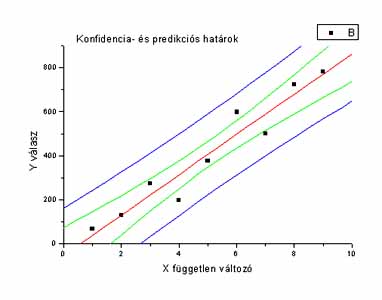
7.1 ábra. Regressziós egyenes és a megbízhatósági
övek. Fekete négyzetek: mért értékek.
Egyenes: regresszós egyenes. Belsõ öv: konfidencia határok,
külsó öv: predikciós határok.
Bármely x* változónál jövõben mért y várható helyének bizonytalansága nagyobb. A jóslási (predikciós) szórás:
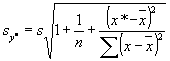 (7.23),
(7.23),
amit a 7.1 ábrán a külsõ öv mutat meg.
A 7.2 ábrát tanulmányozva látható,
hogy hogy az ![]() távolság nem az egyetlen, amelyiket definiálni lehet.
Beszélhetünk az
távolság nem az egyetlen, amelyiket definiálni lehet.
Beszélhetünk az ![]() távolságról,
és az
távolságról,
és az ![]() távolságokról is. Belátható, hogy az
távolságokról is. Belátható, hogy az![]() távolságok
távolságok
![]() (7.24)
(7.24)
négyzetösszege ill. az azokból számított
"modell okozta szórás" arról vall, miért
térnek el az y mért értékek átlaguktól
amiatt, hogy azok x függvényei. Az is érthetõ,
hogy ha ez a szórás összemérhetõ a kisérleti
szórást becslõ, ![]() különbségek
különbségek
![]() (7.25)
(7.25)
négyzetösszegébõl számított
"reziduális szórással", akkor kétséges
a függés léte. Ezért számos esetben a
regressziós számítást variancia analízis
(l. 6. pont) követi, ahol ennek a két szórásnak
négyzetét (varianciáját) F próbával
hasonlítják össze. Minél nagyobb F, annál
biztosabb a függés. Megjegyezhetõ, hogy a modell
okozta eltérésnégyzetösszeg és a reziduális
eltérésnégyzetösszeg kiadja az ![]() távolságok
távolságok
![]() (7.26)
(7.26)
totális négyzetösszegét, mert
![]() (7.27)
(7.27)
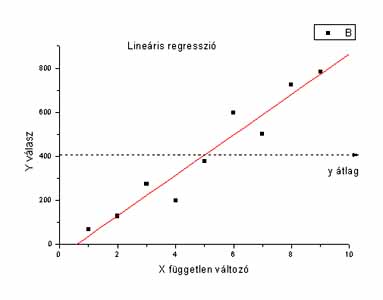
7.2 ábra. A regresszió megítéléséhez
A regresszió jóságát szokás a modell okozta eltérésnégyzetösszeg (7.24) és a teljes (totális) eltérésnégyzetösszeg (7.26) hányadosával is jellemezni.
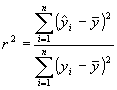 (7.28)
(7.28)
Ez a mennyiség azt adja meg, hogy az y értékek
x-menti
változásának hányadrésze tulajdonítható
a lineárisnak tekintett függésnek. Az r2
hányados az r korrelációs együttható (l.
7.2 pont) négyzete. Nem túl érzékeny mutató.
Ha a mért pontok valamennyien pontosan az egyenesen vannak, értéke
1, de szemmelláthatóan szóró és nem
is lineárisan függõ mért értékeknél
is viszonylag magas (0.9 feletti) lehet.
7.1.3 Nemlineáris paraméterbecslés
Nemlineáris (pl. hatványfüggvénnyel leírható, reciprokos, exponenciális) össszefüggések paramétereinek becslésére a legkisebb négyzetek módszere ugyancsak alkalmazható. Az optimális paramétereket megadó
![]() (7.29)
(7.29)
kritériumban az F függvény nemlineáris , így a deriválás után (ha az lehetséges) kapott (7.8), (7.9) összefüggésekre emlékeztetõ egyenletek nem lineárisak és megoldásukhoz a numerikus matematika erre alkalmas módszerei használhatók.
Egyes esetekben nem kell ehhez a nehéz eljáráshoz folyamodni. Az
![]() (7.30)
(7.30)
függvényben például helyettesíthetünk.
Legyen ![]() .
Ezzel a (7.30) egyváltozós összefüggés az
.
Ezzel a (7.30) egyváltozós összefüggés az
![]() (7.31)
(7.31)
háromváltozós, ám lineáris fügvénnyé
alakult, amelyikbõl a lineáris regresszió szabályai
szerint a keresett paraméterek meghatározhatók. (l.
a 7.16 egyenletrendszert). Hasonlóan lehet eljárni pl. az ![]() modell esetén is.
modell esetén is.
Függvények gyakran úgy linearizálhatók, hogy a transzformáció az y függõ változót is érinti. Az
![]() (7.32)
(7.32)
összefüggés mindkét oldalát logaritmizálva az
![]() (7.33)
(7.33)
lineáris függvényhez jutunk, amelynek paraméterei lineáris regresszióval becsülhetõk.
Az
![]() (7.34)
(7.34)
összefüggés y = ln k és x = 1/T helyettesítéssel lineárissá alakítható.
A mért értékeket érintõ átalakításoknál
azonban figyelni kell arra a következményre, hogy az eredetileg
(alkalmasint) egyenlõ nagyságú hibák a transzformációk
után eltérõkké, sõt esetleg aszimmetrikusakká
válnak, igy a becsült paraméterek torzítottak
lehetnek és hibáikról gondos munka után lehet
nyilatkozni. A súlyozott legkisebb négyzetek módszerének
alkalmazása mindenképpen indokolt.
7.2 Valószínûségi változók összefüggése
Két valószínûségi változó ugyancsak összefügghet. Az összefüggés abban nyilvánul meg, hogy az egyik változó növekedése vagy csökkenése együttjár a másik változó csökkenésével vagy növekedésével. Ezt az összefüggést a kovariancia méri:
C(X,Y) = E[ (X - E(X)) (Y- E(Y))] (7.35)
Ez a mennyiség pozitív, ha az X és Y valószínûségi változók együtt mozognak, negatív, ha ellentétesen. Szokás a kovarianciát a két változó szórásával osztva a - 1 és +1 határok közé szorítani. A kapott mennyiség a korrelációs együttható:
![]() (7.36)
(7.36)
Minél inkább megközelíti r a +1 vagy - 1 értéket, annál szorosabb a két változó közötti összefüggés. Ha el is éri, a két változó egymás lineáris függvénye. Ha a korrelációs együttható 0, akkor a két változó korrelálatlan. Ha két változó független, akkor korrelálatlan is. Fordítva a megállapítás nem érvényes. Attól, hogy r 0-értékû, a két változó között még lehet függvénykapcsolat. Kivételt ez alól a normális eloszlású változók képviselnek.
A korrelációs együtthatót mintából az
 (7.37)
(7.37)
statisztika becsli.
Ha a korrelációs együttható szignifikáns 0 értékét akarjuk megvizsgálni, a
![]() (7.38)
(7.38)
értéket kell kiszámítani. Ha ez nagyobb,
mint ![]() , akkor a
, akkor a ![]() nullahipotézist
nullahipotézist ![]() tévedési valószínûséggel elvetjük.
tévedési valószínûséggel elvetjük.
Korrelált valószínûségi változók lineáris összefüggését lehet regresszióval vizsgálni. A regressziós egyenes azonban más helyzetû, ha Y-t X függvényében, avagy X-et Y függvényéban vizsgáljuk.
Általában fennáll, hogy a korreláció
nem jelent szükségképpen oksági kapcsolatot.
A függõ és független változó fogalma
ebben a környezetben gyakran értelmezhetetlen.
| Tartalom | http://www.chemonet.hu/hun/eloado/stat/
http://www.kfki.hu/chemonet/hun/eloado/stat/ |