(m- us£ x< m+ us) =
(- us £x - m< + us) =
( |x - m| £us)
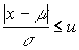
A matematikai statisztika elemei
5. Statisztikai hipotézisek, statisztikai döntések
Az olyan becslések, mint a középérték, a szórás valószínûségi változók, amelyeknek megvan a maguk eloszlása, várható értéke, szórása. Ha ez így van, feltehetõk olyan kérdések, hogy két becslés véletlenül tér-e el egymástól vagy az eltérésnek jelentõs oka van? Más szavakkal fogalmazva kérdezzük: két becslés ugyanahhoz a sokasághoz tartozik-e, azaz, ha számértékük eltér, akkor ez annak tulajdonítható-e, hogy más sokasághoz tartoznak, vagy csak a véletlennek? Ezekre a kérdésekre válaszolnak a statisztikai próbák.
A válaszadás gondolatmenete ez:
(a) meg kell határozni két összehasonlítandó érték eltérését (különbségét).
(b) ha ismerjük a vizsgált valószínûségi változók eloszlását, akkor a két értékkülönbségérõl eldönthetõ, hogy mekkora annak fellépési valószínûsége. Az eltéréseket a különbség szórásához viszonyítjuk, azt vizsgáljuk, nagyobb-e az eltérés ennél a szórásnál, vagy annak két-, háromszorosánál.
(c) ha úgy itéljük, hogy ez a valószínûség kicsiny, akkor az eltérést nem a véletlennek tulajdonítjuk és a két értéket jelentõsen, szignifikánsan eltérõnek nyilvánítjuk, tudva azt, hogy tévedhetünk is. A kis valószínûség szokásosan az a tévedési valószínûséggel egyezik.
Hogy az eltérés mekkora valószínûségét tekintjük majd “kicsiny”-nek (mekkora tévedési valószínûséget vállalunk), az a feladat körülményeitõl függõ, elõzetes elhatározás kérdése. Belátható, hogy a választást a próba elõtt illik megejteni.
A gondolatmenetet és a használt szakkifejezéseket szemléljük meg egy példán. Tegyük fel, hogy arra vagyunk kiváncsiak, egy valószínûségi változó konkrét x értéke beletartozik-e egy, általunk ismert m középértékû és s szórású normális sokaságba vagy nem? Más szavakkal arra, hogy a m-x különbség beesik-e
(- 3s £x - m < + 3s )
tartományba? Ha nem, akkor egy 0.27% valószínûségû esemény következett be. Ha ezt kicsinynek ítéljük, akkor azt mondjuk, x nem tartozik a sokasághoz és ebben 0.27% valószínûséggel tévedhetünk, hiszen elvben végtelen nagy vagy kicsi elem is lehetne a sokaság eleme.
Formálisan ezt tesszük: A
(m- us£ x< m+ us) =
(- us £x - m< + us) =
( |x - m| £us)
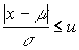
Nos, ha az egyenlõtlenség baloldala, amit ![]() módon is szoktak jelölni nagyobb, mint három, akkor
a
módon is szoktak jelölni nagyobb, mint három, akkor
a
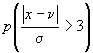 (5.2)
(5.2)Mivel statisztikai vizsgálattal az igazságot abszolut bizonyossággal nem sikerül megállapítani, az állításokat hipotéziseknek nevezzük, és nem azt mondjuk róluk, hogy igazak, vagy hamisak, hanem azt, hogy elfogadjuk-e õket, vagy elvetjük.
5.2.1 Nullahipotézis és alternatív (ellen)hipotézis
Feltevésünk általában az, hogy a vizsgált becslések megegyeznek, azaz különbségük 0. Innen a nullahipotézis elnevezés és a (H0) jelölés
H0: m1 = m2 (5.3)
A nullahipotézissel szemben alternatív hipotézist (HA) szokás felállítani, amely lehet a nullahipotézis ellentéte, de nem szükségképpen az.
HA: m1 ¹m2 (5.4)
vagy például
HA: m1 > m2 (5.5)
5.2.2 Egyoldalas és kétoldalas hipotézisek
Az (5.3) (“egyenlõ”) hipotézissel szembeállított
(5.4) (“nem egyenlõ”) és (5.5) (“nagyobb”) hipotéziseket
meg kell különböztetnünk! Az elsõ esetben elvetjük
a hipotézist akkor is, ha a m1
- m2 különbség túl
nagy negatív, és akkor is, ha ha túl nagy pozitív
szám.
Ha 5% tévedési valószínûséget
választottunk, 2.5% valószínûséget kell
adni annak, hogy a különbség a "haranggörbe" egyik
végére, 2.5%-ot annak, hogy a másik végére
essék. A kérdésfeltevést ezért is nevezik
"kétoldalas" (two sided) feltevésnek. Ha viszont a HA:
m1
> m2 alternatív hipotézissel
foglalkozunk, csak az a határ érdekel, amelynél m1
5% valószínûséggel nagyobb. mint m2.
(Egyoldalas, one sided kérdésfeltevés.) Más
szavakkal: ha kétoldalas a feltevés, azokat az u határokat
figyeljük, amelyek a sûrüségfüggvény
alatti 2.5% - 97.5% valószínûségû területet
határolják, egyoldalas esetben pedig a -¥-
95% valószínûségterületet. A gyakorlatban
ez azt jelenti, hogy a kritikus u értékeket kétoldalas
próbánál a 0.025 (a/2),
egyoldalasnál a 0.05 (a) oszlopban kell
keresni.
5.2.3 Elsõfajú és másodfajú hibák
Statisztikai hipotézisek elfogadásánál vagy
elvetésénél kétféle hibát lehet
véteni: elsõfajú és másodfajú
hibákat:
| Egy igaz hipotézis elfogadása
nincs hiba
Egy igaz hipotézis elvetése elsõfajú, vagy a hiba. Egy hamis hipotézis elvetése nincs hiba Egy hamis hipotézis elfogadása másodfajú vagy b hiba. |
A kétféle hiba jelentõségét csak az adott helyzetben lehet mérlegelni. A körülmények döntik el, hogy mi okoz nagyobb kárt: egy jobb növényvédõszer elvetése, vagy egy rossz bevezetése, egy beteg kezelésének elhagyása, vagy egy egészséges megoperálása. Az elsõfajú hiba valószínûségét a tévedési valószínûség csökkentésével lehet kisebbiteni. A másodfajú hiba valószínûségének beállítása bonyolultabb kérdés.
5.3 Gyakori statisztikus próbák
A továbbiakban két gyakran használt példát mutatunk be. A példák több szempontból egyszerûek, de jó megjegyezni, hogy a matematikai statisztikának a gyakorlatban felvetõdõ nehezebb feladatokra (nem normális, vagy ismeretlen eloszlású adatok, különbözõ mérteû minták stb.) is számos megoldása van.
5.3.1 Két számtani közép egyezésének vizsgálata
Két mérési eredményt akarunk összehasonlítani.
A mérési eredmények véges n1 és
n2 párhuzamos mérés átlagai, számtani
közepek, ![]() és
és ![]() értékek. Tudni szeretnénk, eltér-e egymástól
a két eredmény. Egyszerûség kedvéért
tételezzük fel, hogy a két eredményt ugyanannyi
párhuzamos mért értékbõl számították,
és azt is, hogy a mérési módszer pontossága
a két mérés között nem változott.
Tegyük fel továbbá, hogy a mért értékek
normális eloszlásúak.
értékek. Tudni szeretnénk, eltér-e egymástól
a két eredmény. Egyszerûség kedvéért
tételezzük fel, hogy a két eredményt ugyanannyi
párhuzamos mért értékbõl számították,
és azt is, hogy a mérési módszer pontossága
a két mérés között nem változott.
Tegyük fel továbbá, hogy a mért értékek
normális eloszlásúak.
A nullahipotézis:
H0: m1 = m2 Feltevés : s1 =s2 n1 = n2
Az ellenhipotézis:
HA:m1 ¹m2
A nullahipotézisbõl következik, hogy a vizsgált
valószínûségi változónk a m1
-
m2
küllönbség. Kérdés, mi ennek a különbségnek
a szórása? Tudjuk, hogy az ![]() számtani
közép varianciáját az s2/n
mennyiség becsli. A varianciák összeadhatóságából
következik, hogy az
számtani
közép varianciáját az s2/n
mennyiség becsli. A varianciák összeadhatóságából
következik, hogy az![]() különbség szórása becslése:
különbség szórása becslése: ![]() ,
esetünkben:
,
esetünkben: ![]() .
Aszabadsági
fok: 2*(n-1). Ismerve ezeket a mennyiséget
.
Aszabadsági
fok: 2*(n-1). Ismerve ezeket a mennyiséget
A számított t: 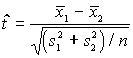
Ezt a mennyiséget kell a táblázati kritikus t(a
,n )-értékkel összemérni.
5.1 Numerikus példa (L. Sachs: Statistische Methoden, Springer, Berlin 1993. p. 77)
Legyen ![]() ,
, ![]()
![]()
t kritikus értéke 95%-os megbízhatósági szinten, 58 szabadsági foknál:
![]()
A m1 - m2 különbség konfidencia tartománya:
2.55 - 2.002 * 1.3661 £ m1 - m2 < 2.55 +2.002 * 1.3661
- 0.1847 £ m1 - m2 < 5.2847
A két középérték nem tér
el egymástól szignifikánsan, H0-t megtartjuk,
a különbség konfidencia tartománya 95% valószínûséggel
tartalmazza 0-t.
5.3.2 Tapasztalati szórások összehasonlítása
Mint errõl a 4.2.3 és 4.2.4 pontban már szó volt, valószínûségi változók négyzetei összegének összehasonlítására célszerûen nem különbségük, hanem hányadosuk eloszlásfüggvénye használtatik. Végesszámú mintákból becsült varianciák ilyen mennyiségek, a döntõ függvény az F-eloszlás. Ha a szórások négyzetének hányadosa meghalad egy bizonyos, a -tól függõ értéket, akkor a két variancia 1 - a biztonsággal eltér egymástól. Az F eloszlás két másik változója a számláló és nevezõ szabadsági foka.
A próba lépései a következõk: Legyen adott 2 minta. A minták elemszáma legyen n1 és n2. A két mintából meghatározunk két standard deviációt: s1-et és s2-t. Kérdés: szignifikánsan eltér-e a két szórás?
1) Fogalmazzuk meg a hipotéziseket:
H0 :![]() HA:
HA:![]() (kétoldalas kérdésfeltevés)
(kétoldalas kérdésfeltevés)
H0: ![]() HA:
HA:![]() (egyoldalas kérdésfeltevés)
(egyoldalas kérdésfeltevés)
2) Válasszunk tévedési valószínûséget (a)
3) Válasszuk ki a két szórás közül a nagyobbat. Kapja ez az 1 indexet.
4) Képezzük a számított ![]() hányadost:
hányadost:
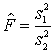 .
.F -nek három változója van: a tévedési valószínûség (a) és a két szabadsági fok: n1 = n1-1 és n2= n2-1.
A kritikus F értékek a táblázatoka
oldalán, a n1 oszlopban és
a n2 sorban találhatók.
Egyoldalas kérdésfeltevésnél az a
valószínüséghez
tartozó táblázatot, kétoldalasnál az
a
/2 valószínüséghez tartozó táblázatot
kell választani. Ha a számított ![]() nagyobb a kritikusnál, a nullahipotézist el kell vetni, a
szórások szignifikánsan eltérnek egymástól,
adott tévedési valószínûséggel.
nagyobb a kritikusnál, a nullahipotézist el kell vetni, a
szórások szignifikánsan eltérnek egymástól,
adott tévedési valószínûséggel.
5.2 Numerikus példa: Elfogadhatjuk-e azt az 5.1 példában megadott hipotézist, miszerint az abban szereplõ szórások megegyeznek? (L. Sachs: Statistische Methoden, Springer, Berlin 1993. p. 77)
H0 :![]() HA:
HA:![]() (kétoldalas kérdésfeltevés)
(kétoldalas kérdésfeltevés)
a= 0.05
![]()
![]()
A nullahipotézist elfogadjuk.
| Tartalom | http://www.chemonet.hu/hun/eloado/stat/
http://www.kfki.hu/chemonet/hun/eloado/stat/ |