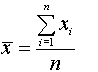 (3.7)
(3.7) |
A matematikai statisztika elemei
3.2 Az adatok eloszlása, a minták jellemzõi
Bár az adatok sorozatának és képének megtekintése bizonyos fokig tájékoztat az adatok elhelyezkedésérõl, szükség van olyan számadatokra, amelyek tömören jellemzik a minta (a) közepét, (b) terjedelmét és (c) eloszlását. Egy-egy célra több jellemzõ közül lehet választani.
A valószínûségszámítás
sokaságok eloszlásának jellemzésére
pontosan definiált mennyiségeket, mint várható
érték, szórás, ferdeség, lapultság,
korrelációs együttható stb. Levezette ezeknek
a mennyiségeknek tulajdonságait is. Az alábbiakban
ismertetett tapasztalati (kisérleti, gyakran statisztikáknak
nevezett) jellemzõk ezeknek az elméleti mennyiségeknek
becslései.
A
becslések között különösen értékeljük
azokat, amelyek torzítatlanok.
Torzítatlan az a becslés,
amelynek várható értéke megegyezik azzal a
mennyiséggel, amelyiket becsül.
a) számtani közép, mintaátlag,
(mean)
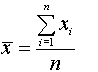 (3.7)
(3.7) |
A számtani közép a hagyományos legkisebb négyzetek elvének megfelelõ jellemzõ, a várható érték torzítatlan becslése. Hátránya, hogy érzékeny a szélsõségesen eltérõ ("kilógó") adatokra.
Az 3.1 példában szereplõ
adatok számtani közepe: - 7.542
A medián az x változó azon értéke,
amelynél a minta elemek fele kisebb, fele nagyobb.
|
A medián nem érzékeny szélsõséges értékekre, u.n. robusztus becslõ.
Az 3.1 példában szereplõ
adatok medánja: 6
|
* több maximumos eloszlásoknál a leggyakoribb, majd a második leggyakoribb... |
A módusz a valószínûségi változó sûrûségfüggvényének maximumhelye. Kisérleti meghatározása nagy mintákból lehetséges, ahol beszélhetünk azonos értékû mintaelemekrõl-rõl.
További, adott esetben hasznos, de gyakorlatunkban ritkábban elõforduló mintaközép jellemzõk még a mértani közép:
![]()
és a harmonikus közép:
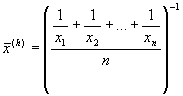
a) standard deviáció (tapasztalati
szórás, korrigált empirikus szórás (standard
error, standard deviation):
Standard deviáció 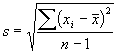 =
=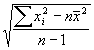 (3.10)
(3.10) |
Ez a jellemzõ az elméleti szórás becslése.
Nevezõjében a kézenfekvõ n helyett azért
szerepel n - 1, mert azt csak
n - 1 független mért
adatból számíthattuk ki. A számtani közép
ugyanis egy adatot az n közül a többibõl kiszámíthatóvá
tesz. Ha a nevezõben
n állna, a standard deviáció
torzítottan becsülné a szórást.
| Fontos megjegyzés: Ha n adat között m darab megkötés létezik, az n adat között csak n - m darab független. A független adatoknak ezt a számát szabadsági foknak (degree of freedom, DF) is nevezik. |
Az 3.1 példában szereplõ
adatok standard deviációja: 98.64
b) variációs együttható
(coefficient of variation)
A variációs együttható azt mutatja meg, hányadrésze, hány százaléka a tapasztalati szórás a középértéknek. Bizonyos esetekben (pl 0 várható értékû sokaságoknál) értelmetlen.
A terjedelem a legnagyobb és legkisebb mintaelem különbsége
| d = xmax - xmin (3.12) |
Az 3.1 példában szereplõ adatok terjedelme: 117 - (-236) = 353
| p-s kvantilis az x változó azon értéke,
amelynél kisebb mintaelemek hányada p.
0.1-es kvantilis = decilis = 10. percentilis 0.25-ös kvantilis = elsõ kvartilis (Q1) = 25. percentilis 0.5-ös kvantilis = második kvartilis (Q2) = 50. percentilis = medián 0.75-ös kvantilis = harmadik kvartilis (Q3) = 75. percentilis 0.90-es kvantilis
= 90. percentilis
|
Az 3.1 példában szereplõ
adatok elsõ kvartilisa -63.5, mediánja 6, harmadik kvartilisa
63.5
A ferdeség
(3.13)
Ez a mennyiség a harmadik centrális momentum/szórás3
módon, a
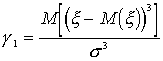
képlettel definiált mennyiség becslése. A ferdeség valószínûségi változóknak különbözõ sûrüségfüggvényei esetén az alábbiak szerint alakul:
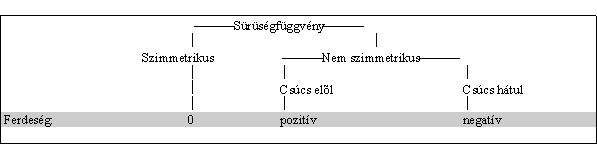
Az 3.1 példában szereplõ
adatok ferdesége: -0.7285
A lapultság:
(3.14)
A lapultság a
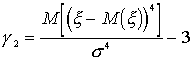
képlettel, g2 = negyedik centrális momentum / szórás4 -3 módon definiált mennyiség becslése.
Ha a lapultság pozitív, akkor a sokaság eloszlásának sûrüségfüggvénye csúcsosabb, mint a normális eloszlás haranggörbéjéé, ha negatív, akkor laposabb, ha 0, akkor egyezõ.
Az 3.1 példában szereplõ
adatok lapultsága : - 0.3232
| Tartalom | http://www.chemonet.hu/hun/eloado/stat/
http://www.kfki.hu/chemonet/hun/eloado/stat/ |