Fizikai Szemle honlap |
Tartalomjegyzék |
Hraskó Péter
Pécsi Tudományegyetem Elméleti Fizika Tanszék
Az alagúteffektus valószínűségének a kiszámítása standard feladat a kvantummechanikában, az effektus időtartamának a meghatározása azonban problémát jelent. Az alagutazási idő fogalmát egy egyszerű gondolatkísérlettel lehet megvilágítani, amelyet egy reális kísérletből kiindulva ismertetek.
Pályakezdőként a KFKI-ban kísérleti magfizikával foglalkoztam. Neutronok rugalmatlan szóródását tanulmányoztuk különféle magokon. A neutronokat a H2+H3 →α +n reakcióban állítottuk elő. Ebben a reakcióban határozott v0 sebességű (14 MeV energiájú) neutronok keletkeznek, de miután rugalmatlanul szóródtak, a sebességük valamilyen kisebb v-re csökken. Ezt a v-t a neutronok repülési ideje alapján határoztuk meg (1. ábra). Azt használtuk ki, hogy a neutronokkal egyidejűleg egy alfa-részecske is keletkezik. Ezt az α-t a keletkezési hely közvetlen szomszédságában elhelyezett detektorral regisztráltuk és a detektor jelét használtuk fel egy óraként működő késleltetett koincidencia-kör megindítására. Az "órát" a neutrondetektor jele állította le. A rugalmatlanul szórt neutronokat több méteres úton repültettük mielőtt a detektorig eljutottak, ezért sebességüket a repülési idejük alapján a szükséges pontossággal meg lehetett mérni. A repülési idő eloszlásából lehetett megállapítani, milyen valószínűséggel gerjed fel különböző energiákra a neutront szóró atommag.
Ha a neutronok útjába nem teszünk be semmiféle céltárgyat, akkor ezzel a módszerrel a H2+H3 → α + n reakcióban keletkező neutronok repülési idejét mérhetjük meg. Tudjuk, hogy energiájuk 14 MeV, amelyből könnyen kiszámíthatjuk, hogy sebességük a fénysebesség körülbelül 17 százaléka: v0 = 0,17 c. Néhány méteres repülési távolság mellett ez nagyságrendileg t0 ≈ 10-7 s repülési időnek felel meg. Semmi meglepetést sem okozott, hogy a kísérlet valóban a sebesség alapján várt repülési időt adta eredményül. Eszünkbe se jutott csodálkozni azon, hogy a repülési idő kiszámításához nem volt szükség kvantumelméletre.
Eddig tartott a reális kísérlet ismertetése. Képzeljük el most, hogy a neutronok útjába makroszkopikus méretű barriert helyezünk el, amely magasabb, mint 14 MeV. Az alagúteffektusnak köszönhetően néhány neutron még így is eljut a neutrondetektorba, de vajon mennyi idő alatt?
A kérdés megválaszolásához a klasszikus kinematika már nem elég, mert a repülési út barrierre eső tartományában a sebesség képzetes. A barrier előtt és után a sebesség továbbra is v0, de ha a barrier kellően széles – mondjuk a teljes repülési távolság fele –, akkor legfeljebb csak azt várhatjuk (de még ebben sem lehetünk egészen biztosak), hogy a repülési idő t0/2-nél nem lesz kisebb. De hogy mennyivel lesz nagyobb, arról fogalmunk sincs. Ez az ismeretlen időtartam az alagutazási idő.
Az évtizedek során több javaslat is született az alagutazási idő kiszámítására. 1955-ben Wigner levezetett egy képletet a rugalmas szóródás időtartamára, vagyis arra az időkésésre, amelyet egy E energiájú részecske szenved el, amikor valamilyen céltárgyon (atommagon) rugalmasan szóródik. A
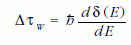
képletet kapta, amelyben δ(E) a rugalmas szórás fázistolása. Azt várjuk, hogy amikor E a céltárgy valamilyen gerjesztett nívójának energiájával egyenlő, ΔτW egyezzen meg a nívó ħ/Γ élettartamával és ez valóban így is van. A képletét Wigner abból a feltevésből vezette le, hogy a részecskét az E-hez közeli energiájú síkhullámokat tartalmazó hullámcsomagként fogta fel és a részecske mozgását a hullámcsomag maximumának a mozgásával helyettesítette. Később a képletet felhasználták az alagutazási idő számítására is, hiszen az alagutazáshoz is határozott δ(E) fázistolás tartozik.1
Egy másik elképzelés szerint a rugalmas ütközés – és az alagutazás – időtartamát úgy lehet megbecsülni, hogy elképzelünk valamilyen homogén mágneses teret, amely a szórócentrum vagy a barrier tartományát tölti ki (ezen kívül zérus), és gondolatban még azt is feltételezzük, hogy a szóródó vagy alagutazó részecskének van valamekkora mágneses dipólmomentuma. Ezután a kvantummechanika alapján kiszámítjuk, hogy a szóródás vagy az alagutazás folyamán mekkora szöggel fordul el a dipólmomentum és a Larmor-formula segítségével ebből meghatározzuk, mennyi ideig tartózkodott a részecske a szórócentrum, illetve a barrier tartományában. Ezt a nagyon mesterkélt ΔτL alagutazási időt nevezik Larmor-időnek. Használatban van egy harmadik, Büttiker–Landauer-időnek nevezett alagutazási idő is, amely talán még a Larmor-időnél is mesterkéltebb. Erre nem térek ki.
Ezek az elképzelések azonban nem lehetnek a végleges válaszok az alagutazási idő kérdésére, mert különböző alagutazási időkre vezetnek és eleve eldöntöttnek tekintenek egy fontos kérdést, azt, hogy az alagutazási időnek határozott értéke van, nem pedig valamilyen valószínűségi eloszlás egy átlagos érték körül. A különböző alagutazási idők közötti választást és az eloszlás problémáját nyilván olyan típusú repülési-időméréssel lehet ellenőrizni, amelyről fentebb volt szó, ezért az emberben elkerülhetetlenül felmerül a kérdés, hogy az alagutazási időt miért nem közvetlenül az alagutazási idő fogalmát operatíve definiáló repülési-időkísérlet várható eredményének kiszámítása útján határozzák meg ahelyett, hogy mesterkélt, másodlagos kritériumokból indulnának ki. Az ok nagyon egyszerű: a kvantumelmélet nem tud mit kezdeni az olyan kísérletekkel, amelyekben részecskedetektorok spontán megszólalásának időbeli eloszlása, illetve korrelációja a vizsgálat tárgya. Ennek az az oka, hogy a |φ(x, t)|2 dt kifejezés nem interpretálható úgy, mint annak valószínűsége, hogy a részecske a (t, t+dt) időintervallumban egy adott x pontban tartózkodik, noha |φ (x, t)|2 dx annak valószínűségét adja meg, hogy egy adott t pillanatban a részecskét az (x, x+dx) intervallumban találjuk meg. Ennek következtében annak valószínűségét, hogy egy részecske a (t, t+dt ) időintervallumban érkezik meg egy adott pontba, csak valamilyen közvetett úton lehet kiszámítani.
Fotonkorrelációs kísérletekben például azt vizsgáljuk, hogy a fénysugár útjában a P1 és a P2 pontban elhelyezett egy-egy (pontszerűnek tekinthető ideális) fotondetektor esetén, mi a w(t1, t2)dt1 dt2 valószínűsége annak, hogy a P1-beli detektor a (t1, t1+dt1), a P2-beli a (t2, t2+dt2) intervallumban szólaljon meg. A kvantumoptikában ezt a valószínűséget a következő eljárással számítják ki.
A detektorokat egy-egy izolált atommal helyettesítik (atomi detektorok), amelyek t = 0-ban alapállapotban vannak. Ezután kiszámítják annak p(t1, t2) valószínűségét, hogy az általunk választott t1-ben az 1. detektort, az általunk választott t2-ben pedig a 2. detektort gerjesztett állapotban találjuk. Ez a számítás elvégezhető a kvantumelmélet standard szabályai szerint, mert az időpontokat mi választjuk. A keresett w(t1, t2) valószínűséget a
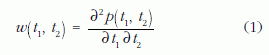
adja meg, mert w(t1, t2) a p(t1, t2) eloszlásfüggvényhez tartozó sűrűségfüggvény: a (t1, t1+dt1; t2, t2+dt2) intervallumban a p (t1, t2) valószínűség annyival növekszik meg, amilyen valószínűséggel a detektorok ebben az intervallumban felgerjednek.
A kvantumoptikában az ilyen típusú gondolatmenettel kapható formulákra a counting rate formula elnevezést használják és a segítségükkel írják le a fotonkorrelációs kísérletek eredményét. Ezekben a kísérletekben a detektorok maguk választják meg azt az időpontot, amikor megszólalnak, és noha a képletek levezetésénél az időpontokat mi jelöljük ki, a tapasztalat szerint ezek a képletek mégis korrekt leírását adják a kísérleteknek. Miért mondtuk akkor, hogy a kvantumelméletben nem tudunk mit kezdeni az olyan kísérletekkel, amelyekben a detektorok spontán megszólalásainak korrelációjára kérdezünk rá?
Azért, mert (1) nem garantálja, hogy a w(t1, t2) valószínűségre pozitív értéket kapjunk. A kvantumelméletben ugyanis nincs ok arra, hogy a p(t1, t2) valószínűség az argumentumainak monoton növekvő (vagy legalább is nem csökkenő) függvénye legyen. A "szokásos" kvantumelméleti valószínűségek pozitivitását a kiszámításuk algoritmusa biztosítja (wn = |(φn, ψ)|2). Az időbeli eloszlások számításának előbb vázolt receptje ezt nem garantálja – kivéve, ha a foton és a detektor-atom kölcsönhatás első rendjére (az első Born-közelítésre) korlátozódunk. A kvantumoptikában a foton és a detektor kölcsönhatás számításánál mindig ezt a közelítést használják, mert – hacsak nem tiltja valamilyen kiválasztási szabály, – az első Bornközelítés általában jó közelítést ad.
A gondolatmenet azért eredményezhet negatív valószínűséget is, mert azt az állítást, hogy "a detektor megszólalt" azzal az állítással helyettesítettük, hogy "a detektor-atom gerjesztett állapotban van". A két állítás nem egyenértékű. Az, hogy a detektor megszólalt, irreverzibilis kijelentés, amely nem tehető meg nem történtté. A detektor-atom a valóságban ugyanis nem egy izolált rendszer, hanem egy makroszkopikus eszköz része, amely képes jelezni a gerjesztés tényét. Egy izolált atom esetében azonban a dinamikai egyenlet megengedi, hogy az atom gerjesztettsége időben csökkenhessen (az alapállapoti valószínűség növekedjen). Ez csak az első Born-közelítésben nem fordulhat elő.
Elég nyilvánvaló, miről van itt szó. A detektor megszólalása spontán redukciós folyamat, amelyet a Schrödinger-egyenlet – mint tudjuk – nem ír le. Ezt a spontán redukciós folyamatot kell valahogy megkerülni ahhoz, hogy az időbeli korrelációkat tárgyalni tudjuk. Ez a megkerülés történik meg
a detektor megszólalt →
a detektor-atom gerjesztett állapotban van
helyettesítéssel, amelyet naiv redukciós hipotézisnek fogok nevezni. A kvantumelméletben mindig, amikor időbeli eloszlásokról van szó – az exponenciális bomlástörvény tárgyalásánál például –, tudatosan vagy hallgatólagosan a naiv redukciós hipotézist alkalmazzák.
Tegyük fel a kvantumoptikai tapasztalatok alapján, hogy a naiv redukciós hipotézis a Born-közelítéssel kombinálva elfogadható közelítése a spontán redukció ma még ismeretlen pontos elméletének és próbáljuk felhasználni az alagutazási idő kiszámítására. Nyilvánvaló ugyanis, hogy az alagutazási idő is két spontán esemény időbeli korrelációjával kapcsolatos, ezért a kvantumoptika gyakorlatát erre a feladatra is alkalmazhatjuk, hacsak fotonokkal is végezhetünk alagutazási kísérletet.
Ezért fontos körülmény, hogy lehet készíteni olyan fóliákat, amelyek fotonbarrierként viselkednek. A Maxwell-egyenletek – amelyek a foton Schrödinger-egyenletének a szerepét töltik be – az ilyen fólia jelenlétében matematikailag pontosan azonosak a nemrelativisztikus részecskék alagutazását leíró Schrödinger-egyenlettel (nulla spinű fotonra), ezért remélhető, hogy ha mélyebben belelátunk a foton-alagutazás tulajdonságaiba, a részecskék alagutazásáról is megtudhatunk valamit.
Az időkorrelációs felfogás szellemében a fotonok alagutazási idejét a következő eljárással kell kiszámítani:2
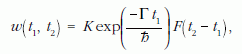
amelyben Γ a forrás-atom nívószélessége, K pedig egy konstans, amely a forrás bomlási állandóját, a barrier transzmisszióját, valamint az elrendezés geometriájával összefüggő mennyiségeket tartalmazza.
Amikor barrier nincs jelen, F(t2-t1) = δ(t2-t1-z /c)-re jutunk, ami a várakozásnak megfelelően azt fejezi ki, hogy a foton pontosan fénysebességgel teszi meg a z távolságot. Ez az eredmény a számítási eljárás fontos kontrollja, és valószínűleg az első olyan számítás, amely – a tett feltevéseken belül – igazolja, hogy a fény a kvantumelektrodinamika szerint is c sebességgel terjed a vákuumban. Érdekes kérdés, hogy vajon ilyen számítást el lehet-e végezni neutrínókra, és ha igen, azt kapjuk-e eredményül, hogy a neutrínók a kvantumtérelmélet szerint is pontosan fénysebességgel mozognak. Egy ilyen vizsgálat az OPERA-kollaboráció nagy figyelmet keltő eredményei kapcsán különösen aktuálissá vált. Mint jól ismert, ez a kísérleti csoport arról számolt be, hogy 730 kilométeres bázistávolságon végzett megfigyeléseik szerint a neutrínók a fénynél gyorsabb sebességgel haladnak. Ezt két egymás utáni mérésben is tapasztalták, amelyek közül a második a jelen cikkben tárgyalt repülésiidő-kísérlethez volt hasonló.3
Széles és magas barrier esetében a fenti számítás az F(t2-t1) = δ(t2-t1-(z-D)/c) képletre vezet, amelyből az következik, hogy az alagutazás nem vesz időt igénybe (végtelen sebességgel történik) és a vizsgált határesetben az eloszlása éles. Mindjárt egy kicsit részletesebben diszkutálom ezt a következtetést, de előbb megjegyzem, hogy a naiv redukciós hipotézisen túlmenő közelítések miatt nem ezt a számszerű eredményt, hanem a gondolatmenetet tartom a számításban a legfontosabbnak. Hangsúlyozom még, hogy a számítás során nem szükséges – és nem is lehet – figyelembe venni olyan addicionális kritériumokat, amilyenek például a Wigner-időhöz vagy a Larmor-időhöz szükségesek. Az időkorreláció-számításnál a barrier abban jelentkezik, hogy az elektromágneses mező módusai nem pontos, hanem a barrier által deformált síkhullámok, pontosan olyanok, mint a határozott energiájú részecskék alagutazásának a tárgyalásánál fellépő hullámfüggvények.
A 2. ábrán a két függőleges vonal a forrás és a detektor-atom világvonala, E1 a bomlási, E2 pedig a detektálási esemény. A két pontot összekötő szaggatott vonal a foton pályáját reprezentálja. A középső szakasz vízszintes, mert a számítás szerint az alagutazás nem vesz igénybe időt. Ennek ellenére a rajzon feltüntetett viszonyok mellett a kauzalitás nem sérül, mert az E1 esemény időpontja nem a kísérletező választásától függ. A kísérletező utoljára az E esemény, az állapotpreparálás alkalmával avatkozik be a rendszerbe, ezért az információ E és E2 között terjed. Mivel E2 az E fénykúpján belül van, az információ terjedési sebessége kisebb a fénysebességnél.
Ez természetesen azon múlik, hogy a rajzon a bomlás a D/c időnél később következik be: t1 > D/c. Amikor t1 < D/c, az E2 az E fénykúpján kívülre kerül. A számítás azonban ezt az esetet nem öleli fel, mert Wigner– Weisskopf-közelítésben történt, amelyről ismeretes, hogy a ħ/Γ bomlási időnél sokkal kisebb időkre nem érvényes. Ezért, amikor arra a következtetésre jutunk, hogy E2 az E fénykúpján vagy azon kívül van, a Wigner–Weisskopf-közelítésnél pontosabb kiértékelési eljárás válik szükségessé, amely lényeges módosításhoz vezethet. Nagyon jó lenne tudni, hogy a pontosabb tárgyalás megengedi-e, hogy E2 az E fénykúpján kívülre kerüljön. Amikor azonban E2 kellő mértékben az E fénykúpján belül van (t2-z/c >> ħ/fotonenergia), a Wigner–Weisskopf-közelítés elfogadható.
Összefoglalva: az alagutazási időt a fogalom definíciója alapján a foton emissziójának és abszorpciójának időkorrelációjából lehet meghatározni. A kvantumelmélet azonban jelenleg nem biztosít egy ilyen számításra fundamentális elveken alapuló eljárást; úgy látszik, ez a kvantumelmélet egyetlen még ma is megoldatlan problémája. Ha a kvantumoptika gyakorlatából indulunk ki, amely a naiv redukciós hipotézisen alapul, akkor a kísérletező utolsó beavatkozásának fénykúpján belül az alagutazási idő standard kvantumelektrodinamikával kiszámítható..
___________________