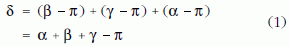
Fizikai Szemle honlap |
Tartalomjegyzék |
Bokor Nándor, BME Fizika Tanszék
Laczik Bálint, BME Gyártástudomány és -technológia Tanszék
Mikor párhuzamos két vektor? A válasz magától értetődőnek tűnik: ha ugyanabba az irányba mutatnak. Menjünk tovább: szeretnénk egy vektort a sík adott pontjából egy másikba párhuzamosan elmozgatni. Körülményesebbnek tűnő megfogalmazással: szeretnénk apró lépésenként úgy odébb vinni, hogy mindegyik lépés végén kapott vektor párhuzamos legyen a lépés kiinduló vektorával. Így joggal várhatjuk, hogy a teljes művelet végén kapott vektor is párhuzamos lesz a kezdeti vektorral. A mozgatási szabály ismét magától értetődőnek tűnik (legalábbis sík felületen): úgy kell a vektort elmozgatni, hogy közben mindig az eredeti irányba mutasson (1. ábra).
De mi a helyzet görbült felületen? Hogyan magyarázzuk el például egy gömb felületén élő "laposlényeknek" (akik számára nem létezik a harmadik dimenzió, nem látnak ki a felületből), hogy mi a teendő, ha a saját világukban egy vektort párhuzamosan akarnak eltolni? A precíz matematikai szabályt előbb saját magunknak kell kiokoskodnunk, hogy aztán tudathassuk kétdimenziós barátainkkal. Világos, hogy az "úgy eltolni, hogy végig a [3-dimenziós értelemben] eredeti irányba mutasson" szabály itt nem működik, hiszen akkor a vektorok előbb-utóbb kifordulnának a felületből. Márpedig a laposlények vektorai mind a felület érintősíkjában állnak; különben olyan irányú komponensük is lenne, amely dimenzió nem is létezik (a laposlények számára).
Nézzünk először néhány könnyen tárgyalható konkrét esetet a gömbfelületen, aztán próbáljuk meg megfogalmazni az általános szabályt. A 2. ábra egy gömbfelületet, a laposlények univerzumát ábrázolja. Lapos barátaink szeretnének az A, B és C jelű görbéken párhuzamos eltolással körbevinni egy-egy olyan vektort, amelyek a kiinduláskor az adott görbével érintő irányúak. Ezt az első gondolatkísérletünket célszerű úgy megválasztanunk, hogy mindhárom görbe szabályos kör legyen. A nyilvánvaló analógia miatt szemléletes úgy gondolni ezekre, mint Földünk különböző szélességi köreire: az A jelű közel van az Északi Sarkhoz, a B jelű valahol az északi félteke közepe táján helyezkedik el, a C jelű pedig maga az Egyenlítő. Próbáljuk berajzolni az ábrába, hogyan néznek ki a három esetben az apró lépésenként párhuzamosan eltolt vektorok!
Az A görbe esetén a legegyszerűbb a dolgunk. A bejárt tartomány a teljes gömbnek nagyon kicsi része, amelyről tudjuk, hogy gyakorlatilag síknak tekinthető. Ahogy egy stadionban körbefutó atléta mozgásának elemzéséhez sem kell a Föld görbületét figyelembe vennünk, úgy itt is minden további nélkül alkalmazható a síkbeli szabály: ábránkat úgy kell megrajzolni, hogy az összes eltolt vektor "nézzen ugyanabba az irányba" (3. ábra). A vektor tehát előbb kifordul az A görbéből, aztán a teljes kör megtétele után visszajut eredeti állapotába. Az eredeti vektor és a teljes kör megtétele után visszajutott vektor 0 fokos szöget zár be egymással, ahogy síkbeli rajzaink tapasztalatai után várjuk.
A C görbe esete is egyszerű. Először is, az ábrára a "párhuzamosan eltolt" vektorokat úgy kell berajzolnunk, hogy végig a felület érintősíkjaiban maradjanak (hiszen a laposlények számára csak ilyen vektor értelmezhető). Másodszor, mivel a C görbe a gömb egyenlítője, amely szimmetrikusan osztja két részre a gömböt, érintővektora a "párhuzamos eltolás" folyamán nem fordulhat ki sem lefelé, sem felfelé a görbéből, különben megsértené az ábra szimmetriáját. (Akár a lefelé, akár a felfelé elfordulást választjuk, nem tudnánk választásunkat megindokolni.) A vektor tehát mindvégig a görbe érintővektora marad (4. ábra). Mint az A görbe esetében, a vektor a kiindulópontba visszajutva ekkor is fedésbe kerül eredeti helyzetével, de most közben - kívülről, a 3 dimenziós térből nézve - tett egy teljes kört (ebből a nézőpontból nem igaz tehát, hogy mindvégig "ugyanabba a irányba mutatott"!). Helyesebb ezért, ha úgy fogalmazunk: az eredeti vektor és a teljes kör megtétele után visszatért vektor 2??szöget zár be egymással.
Az A és a C görbe esete markánsan különbözik egymástól: az A görbe mentén - jó közelítéssel sík felületen - végigvitt vektor a teljes kör megtétele után is ugyanabba az irányba mutat, bár menet közben a görbéből erősen kifordul. A C görbe mentén végigvitt vektor viszont a görbéhez képesti helyzetét őrzi meg, miközben a külső (3 dimenziós) szemlélő számára drasztikusan változtatja az irányát. Szerencsés véletlennek tűnik, hogy a teljes kör megtétele után éppen 2π-nek adódik az összes szögelfordulás.
A B görbe közbülső eset. Eddigi tapasztalataink alapján a következőképpen okoskodhatunk: a vektor a párhuzamos eltolás során biztosan ki fog fordulni a görbéből (hiszen nem alkalmazható rá a C görbénél indokolt szimmetria-érvelés), de nem olyan mértékben, mint az A görbe esetén (5. ábra). Bár okoskodásunk hibátlan, a kapott ábra mégis bántóan ellentmond az ösztöneinknek. A berajzolt vektorok egyszerűen "nem tűnnek párhuzamosnak"; ráadásul az a zavarba ejtő furcsaság adódik, hogy a kiindulási vektor és a teljes kör után ugyanoda érkezett eredmény-vektor nyilvánvalóan egészen más irányba mutatnak.
Mielőtt pontosan megértenénk, miért történik ez, gondoljuk végig a következőket: a gömb olyan alakzat, amelynek minden pontja egyenértékű. A B görbén végigvitt vektor furcsa viselkedéséért tehát a bejárt görbe a felelős, nem pedig a kiindulópontnak a gömbön elfoglalt helyzete. Ha ugyanabból a kiindulópontból ugyanazt a vektort egy kis tartományon hordoztuk volna körbe (mondjuk egy az A-hoz hasonló kör mentén), a végeredményül kapott vektor biztosan fedésbe került volna a kiindulási vektorral (6. ábra). Gondolkodjunk el ezek után, milyen általános szabályt tudunk megfogalmazni, amely a szemléletünknek is megfelel, és az 5-6. ábrák furcsaságait is megnyugtatóan magyarázza. Érezhetjük, hogy naiv szabályunkkal mi volt az egyik baj: a "mindig ugyanarra mutasson" követelmény csak a vektorokról mond egy (ráadásul eléggé pongyolán megfogalmazott) állítást, a görbéről, amely mentén a vektort eltoljuk, tudomást sem vesz. A gömbi példákból viszont láttuk, hogy a vektor helyzetét ahhoz a görbéhez képest kell megadni, amely mentén odébb visszük.
Térjünk vissza oda, ahol a legnagyobb biztonságérzettel mozgunk: egy sík felületre. Először toljuk el vektorunkat párhuzamosan egy egyenes mentén (7. ábra). Megfigyelésünk egyszerű: az eltolás során a vektor a bejárt egyenes vonallal mindvégig azonos szöget zár be. (Érezzük, miért nagy lépés ez: a felület két vonala közötti szög a laposlények számára is könnyen értelmezhető, ellentétben a kissé megfoghatatlan "ugyanarra mutasson" szabállyal.) Új szabályunk tehát: "Ha egyenes mentén akarod párhuzamosan eltolni a vektorodat, akkor lépésről lépésre gondoskodj arról, hogy a vektor mindvégig azonos szöget zárjon be az egyenessel." A biztonságot adó sík felületen most görbe vonal mentén vigyük végig a vektort (8. ábra). A görbével bezárt szög nyilvánvalóan változik. Előbb felállított szabályunkat mégis átmenthetjük erre az esetre, az alábbi módon: "Ha görbe mentén akarod párhuzamosan eltolni a vektorodat, akkor a görbét közelítsd kicsiny egyenes szakaszokkal - ezek adják az eltolás lépéseit -, és minden kicsiny egyenes szakaszra követeld meg, hogy a szakasz elején és végén a vektor azonos szöget zárjon be az adott egyenes szakasszal" (8. ábra). Másodikként felállított szabályunk természetesen önmagában is megállja a helyét, hiszen az egyenes mentén történő eltolás speciális esetként kiadódik belőle. De alkalmas-e arra, hogy görbült felület (például gömb) felületén élő laposlényeknek használható receptet adjon a párhuzamos eltolásra? Egyetlen apró átfogalmazásra van csak szükség: az "egyenes" szó görbült felület esetén homályos értelmű, ezért cseréljük ki az általánosításaként használt "geodetikus" szóval. (A geodetikus definíciója: a két adott pontot összekötő vonalak közül a legrövidebb.)
Összefoglalva tehát eddigi tapasztalatainkat, bármilyen felületen élő laposlényeknek a következő eltolási szabályt adjuk:
Ha adott vonal mentén párhuzamosan akarod eltolni a vektorodat, akkor a vonalat közelítsd kicsiny geodetikus szakaszokkal - ezek adják az eltolás lépéseit -, és minden kicsiny geodetikus szakaszra követeld meg, hogy a szakasz elején és végén a vektor azonos szöget zárjon be az adott geodetikus szakasszal.
Ellenőrizzük szabályunk használhatóságát a gömbi laposlények esetére! Ismert (és a laposlények is tudják), hogy gömbfelületen két pont közötti legrövidebb út főkör mentén vezet: a főkörök a gömbfelület geodetikusai. A 2. ábra C görbéje pontosan ilyen. Szabályunk azt diktálja, hogy például az ilyen görbe érintővektorának párhuzamos eltoltja mindvégig a görbe érintővektora maradjon. És valóban: a 4. ábra megrajzolásakor - más megfontolásból kiindulva - pontosan ezt az eredményt kaptuk. Ami még ennél is meggyőzőbb: szabályunkat a B görbe mentén való eltolásra következetesen alkalmazva valóban az 5. ábrán látható, elsőre furcsának tűnt viselkedést kapjuk. (A repülés történetének jelentékeny eseménye volt, amikor a légitársaságok rádöbbentek, hogy az azonos szélességi körön fekvő városok - például New York és Isztambul - között nem az őket összekötő szélességi kör mentén érdemes repülni, mert nem az a legrövidebb út.) Természetes, hogy a vektor kifordul a B szélességi körből, hiszen ez a szélességi kör görbe vonal a gömbön, amit "egyenes" (= geodetikus) szakaszokkal kell közelítenünk. A szabályunk alkalmazását illusztráló 9. ábra tulajdonképpen a 8. ábra megfelelője gömbfelületre.
Már tudjuk, hogy a vektor teljes szögelfordulása, miután zárt görbén párhuzamos eltolással visszavittük eredeti helyzetébe, függ a görbe alakjától, az általa bezárt terület nagyságától. De mekkora ez a teljes szögelfordulás? Ezt a kérdést a Gauss-Bonnet-tétel válaszolja meg, amelynek Eulertől származó elegáns bizonyításváltozatát [1] az alábbiakban vázoljuk.
Görbült felületre éppúgy rajzolhatunk sokszögeket, mint síkra, csak a sokszög síkbeli definícióját - egyenes szakaszokkal határolt alakzat - kell értelmesen módosítanunk: a sokszög geodetikus szakaszokkal határolt alakzat. Példaként a 10. ábra egy gömbfelületre rajzolt háromszöget mutat. Mindhárom oldal a gömb geodetikusának - azaz egy-egy főkörének - darabja. Vigyünk körbe egy vektort a gömbi háromszögön a párhuzamos eltolás szabályának megfelelően. Mint láttuk, geodetikus vonal mentén párhuzamosan eltolt vektor megtartja a geodetikushoz képesti irányát (4. ábra). Mivel alakzatunk csupa geodetikus vonalból áll, a párhuzamos eltolás ábrája könnyen megrajzolható. Az egyszerűség kedvéért az A-ból kiinduló vektor legyen az AB oldal érintővektora. Érintő irányát megtartja egészen addig, amíg a B csúcshoz ér. Ott a BC oldallal β–π?szöget zár be (úgy is mondhatjuk, hogy az AB oldallal bezárt 0°-os szöghöz ekkora szögnövekmény adódik), és ezt a szöget a BC oldalon való végighaladás során mindvégig megtartja. Amikor a C csúcshoz ér, és elindul a CA oldalon, újabb, ezúttal (γ–π) nagyságú szögnövekményt kap, azaz a BC oldallal bezárt szöge (β–π) + (γ–π) lesz. Végül az A csúcshoz, azaz a kiinduló ponthoz érve az AB oldallal - és saját eredeti irányával - bezárt szöge immár (β–π) + (γ–π) + (α–π) lesz.
A vektor a teljes hurok megtétele után tehát
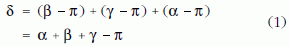
szögelfordulást végez (a szögelfordulást "moduló 2π" értelmezzük, tehát 2π ?többszörösei elhagyhatók).
A képlet gyors ellenőrzése: síkháromszög esetén α+β+γ? = π, tehát δ-ra zérus adódik, amint egy sík felületen párhuzamosan eltolt vektortól el is várjuk.
Tegyünk fel egy látszólag nem ide tartozó kérdést: mekkora a 10. ábrán látható gömbi háromszög területe? A válaszhoz rajzoljuk le a háromszöget még egyszer, de úgy, hogy az oldalakat adó főköröket végig kirajzoljuk (11. ábra). A három főkör - ezt egy gumilabdán, a főköröket golyóstollal berajzolva könnyen ellenőrizhetjük - a gömbfelületet nyolc részre osztja. Ha ezek közül kiválasztunk négyet: az eredeti ABC gömbháromszöget, valamint az AB, a BC és a CA oldalakkal érintkező további 1-1, összesen három gömbháromszöget - lásd a vonalkázott részeket a 11. ábrán -, érdekes megfigyelést tehetünk (segít a már említett gumilabda): a bevonalkázott rész a gömb felületének éppen a felét fedi le, sőt egybevágó a be nem vonalkázott maradék résszel. A vonalkázott terület tehát
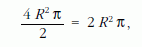
ahol R a gömb sugara.
Az ábrán az is látszik, hogy az ABC háromszög voltaképpen három elnyújtott (és bevonalkázott) "kifli- alakzat" metszet-tartománya. Mindhárom kifli-alakzat úgynevezett gömbi kétszög (az elnevezés teljesen logikus; mindazonáltal ennek az egzotikus sokszögnek hiába keresnénk a síkbeli megfelelőjét, ott ugyanis két egyenes nem metszheti egymást kétszer.) A gömbi kétszög egy narancsgerezd héjához hasonlít, ezért területének kiszámítása magától értetődő: területe a gömbfelületnél annyiszor kisebb, ahányszor kisebb a nyílásszöge 2π-nél. A 11. ábrán bevonalkázott, A csúcsú kétszög területe például:
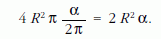
Az ABC gömbi háromszög T területét ezek után a következő gondolatmenettel kaphatjuk meg: ha a három gömbi kétszög területét összeadjuk, majd az eredményből kétszer kivonjuk a triplán figyelembe vett ABC gömbháromszög területét, megkapjuk a bevonalkázott összterületet:
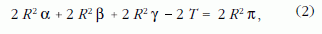
amiből a gömbháromszög területe:
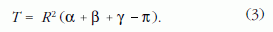
A (3) és (1) egyenletek egybevetésével azonnal látjuk, hogy párhuzamosan körbevitt vektor teljes δ ?szögelfordulása a bejárt területtel arányos:

(Innen adódik a δ-ra gyakran használt felületi excesszus elnevezés.)
Ahogyan egy szöghöz tartozó körívhossz osztva a kör sugarával adja a radiánban mért szög definícióját, úgy a szteradiánban mért térszög definíciója: a térszöghöz tartozó gömbfelület -darab osztva a gömb sugarának négyzetével. A (4) egyenlet jobb oldalán tehát éppen az ABC gömbháromszöghöz tartozó Ω térszög szerepel, azaz a végeredmény ebbe az egyszerű alakba írható:

Szavakkal: a gömbi háromszög mentén párhuzamosan eltolt vektor teljes felületi excesszusa (radiánban mérve) egyenlő a háromszög által lefedett (és szteradiánban mért) térszöggel.
A (4) egyenlet könnyen általánosítható: érvényessége igazolható előbb tetszőleges gömbi sokszögre, majd tetszőleges zárt görbére a gömbfelületen. Egy gömbi sokszög ugyanis felbontható gömbi háromszögekre (12. ábra). Könnyen belátható, hogy a teljes felületi excesszus megkapható, mint a háromszögekhez tartozó felületi excesszusok összege. Ugyanakkor - triviális módon - a teljes terület is a háromszögek területének összegeként adódik. A (4) egyenlet tehát változatlan formában igaz. Másrészt a gömbfelületen tetszőleges zárt görbe közelíthető - tetszőleges pontossággal - gömbi sokszöggel, azaz a (4) egyenlet a gömb felületén valóban tetszőleges görbére igaz.
Gaussnak a görbült felületek geometriájában elért egyik legfőbb eredménye az volt, hogy talált egy olyan mérőszámot - ezt tiszteletére Gauss-görbületnek nevezzük -, amely egyértelműen és pontról pontra jellemzi az adott felület görbültségének mértékét [2]. A probléma nehézsége abból adódik, hogy a görbület-mérőszámtól elvárjuk: a felület deformációmentes változtatása - mint például egy sík lap felgörgetése hengerré - "ne tudja becsapni": egy újságlap a lényegét tekintve akkor is sík felület, amikor legyet akarunk vele agyonütni.
A Gauss-görbület kiszámításának módját a következő gondolatkísérlet illusztrálja: az adott pontban húzzuk meg a felület érintősíkját. Állítsunk erre az érintősíkra merőleges síkokat az összes létező irányban. Ezeknek a merőleges síkoknak és a görbült felületnek a metszésvonalai síkgörbék, amelyeknek az adott pontban meghatározható a görbületi sugaruk. A végtelen sok merőleges síkhoz végtelen sok síkgörbe tartozik, mindegyikhez 1-1 görbületi sugár. Ezeket a görbületi sugarakat előjelesen értelmezzük, attól függően, hogy az adott érintőkör középpontja a felület "alatt" vagy "fölött" helyezkedik-e el. A végtelen sok görbületi sugár érték között lesz egy (előjelesen) legkisebb és egy legnagyobb: Rmin és Rmax. Gauss zseniális meglátása az volt, hogy a
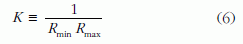
mennyiség tökéletesen megfelel a céloknak. Igazi mérőszáma a felület adott pontban értelmezett görbületének, ráadásul előjeles mennyiség. Nem csak síkra, hanem - a sík felületté torzításmentesen kiteríthető - hengerfelületre is zérust ad (utóbbi esetben Rmax = ∞ ?miatt) Nyeregfelületre negatív szám, gömbfelületre pozitív. Hangsúlyozandó, hogy K, a Gauss-görbület, pontról pontra értelmezett mennyiség, csak éppen gömbfelület esetén minden pontra ugyanaz: K = 1/R2. Ez utóbbi összefüggéssel a (4) egyenlet a következő alakba írható:

Ez a felírásmód csak állandó görbületű felületekre (a gömbre, és a később tárgyalandó pszeudoszférára) alkalmazható. Tetszőleges görbült felületre így általánosítható: a felületen, adott zárt görbe mentén párhuzamosan eltolt vektor teljes felületi excesszusa egyenlő a Gauss-görbületnek a görbe által körülzárt felületre számított integráljával:

Ez a Gauss-Bonnet-tétel.
Érdekesség, hogy a Gauss-Bonnet-tételnek az (5) egyenlet változtatás nélkül, általánosan használható alakját adja. Ilyenkor, tetszőleges (nem gömbi) görbült felület esetén, az (5) jobb oldalán szereplő Ω ? térszöget a 13. ábra szerint értelmezzük: amint a görbült felület normál egységvektora végigvándorol a G zárt görbén, ugyanezek a normál egységvektorok egy egységgömb középpontjából kiindítva egy másik zárt görbét írnak le az egységgömb felületén. Ennek az egységgömb felületén kialakult zárt alakzatnak a területe adja Ω-t (egyben a G görbéhez tartozó δ ?felületi excesszust, egyben az eredeti görbült felület Gaussgörbületének a T felületre számított integrálját).
A 13.a ábra az
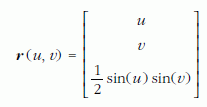
felületet és az –0,8 ≤ ?u ≤ ?0,7, –1 ≤ v ≤ ?1,1 tartomány határán az
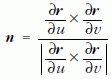
normál egység vektorokat szemlélteti, a tartomány úgynevezett gömbi képét (azaz az egység sugarú gömb középpontjából indított normál egységvektorok végpontjai által kijelölt alakzatot) pedig a 13.b ábra mutatja.
Szellemes technikai megoldásokkal vagy egyszerű fizikai elvek kihasználásával többféle olyan eszköz konstruálható, amelyek - adott felület adott görbéje mentén elmozogva - ténylegesen megvalósítják vektorok párhuzamos eltolását. (Itt a "vektort" például egy a felület érintősíkjában adott irányban álló rúdnak képzeljük el, amely az eszköz többi részéhez képest elfordulhat, de mindig a felület érintősíkjában marad.1) Az ilyen eszközökkel kétféle alapkísérlet is végezhető: (1) adott felületen adott zárt görbe mentén végigtolva az eszközt, a "vektor" teljes elfordulásából megkapható a felületi excesszus, és így belső méréssel meghatározható az integrált Gauss-görbület; (2) ügyeskedve úgy végigtolva az eszközt a felületen, hogy a "vektor" orientációja (az eszközhöz képest) ne változzon, meg lehet találni a felület geodetikus vonalait.
A délirányt jelző kordé [3-5] nevű ókori kínai találmány - egyes feljegyzések szerint i.e. 2634-ben (!) találta fel a "Sárga császár", a nagy birodalom akkori uralkodója - a kietlen terepen utazók tájékozódását segítette. Szerkezetének legfontosabb része egy briliáns műszaki lelemény, a fogaskerék differenciál (amely a gépkocsik mindmáig fontos szerkezeti része). A délirányt jelző kordé egy, a British Museumban kiállított modellje a 14.a ábrán látható. A működő szerkezet felső részén álló szobor kinyújtott karja a jármű mozgásirányától függetlenül állandó irányba mutatott. (A kordé indulásakor tetszőleges alapirányt lehet választani, a korabeli kínai navigáció szerint azonban a figura a déli világtájat jelezte.)
A 14.b képen egy általunk készített modell látható. Az interneten számos LEGO-változat található, ezek egyikét is összeraktuk (14.c ábra).
A szerkezet eredeti verziójának egyszerűsített vázlatát a 15. ábra szemlélteti. Az eredeti mechanizmusban a fogaskerekek legrégebbi alakjai, az úgynevezett homlokcsapos vagy pálcás fogazatok találhatók. Az a és b jelű, azonos átmérőjű kerekeken gördül a szekér; a bal és jobb oldali kerekek szögsebessége ω2, illetve ω1. A fogaskerekek azonos átmérőjűek, homlokfelületükön megegyező osztású pálcákból épülnek fel. A koronaszerű kialakítás lehetővé teszi mind a párhuzamos, mind a merőleges tengelyelrendezésű kerekek kapcsolódását (16.a ábra). (Az ábrán a fogaskerekek tengelyeit nem tüntettük fel.)
Azonos alakú fogaskerekek esetén a bal oldali kordékerék a hozzákapcsolt b', a két részből álló c, valamint az f jelű fogaskerekeket ω2 szögsebességgel hajtja. Hasonlóképpen a jobb oldali kerék a vele összekapcsolt a', valamint a mindkét homlokfelületükön fogazott d és e jelű fogaskerekeket ω1 szögsebességgel forgatja. A felsorolt kerekek mindegyike a szekérhez rögzített tengelyek körül foroghat.
A csúszás nélkül gördülő, azonos ρ ?sugarú kerekek talajjal éppen érintkező pontjai pillanatnyi nyugalomban vannak, a kerekek középpontjai pedig v1 = ω1ρ, illetve v2 = ω2ρ ?sebességgel mozognak (16.b ábra). Ha például ω1 < ω2, a jármű a P pont körül Ω?szögsebességgel elfordul:
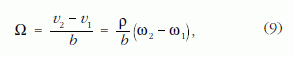
ahol b a kerekek nyomtávolsága.
A szerkezet legérdekesebb része az e, f, g és g' jelű fogaskerekekből felépülő differenciálmű (17. ábra).
Az e és f fogaskerekek a kordéhoz rögzített függőleges tengely körül foroghatnak, a g és g' kerekeket hordozó vízszintes tengely azonban az e és f kerekek közös tengelyvonala körül képes elfordulni. A g és g' kerekeket hordozó vízszintes tengelyhez kapcsolódik az állandó irányt jelző h kar. Az f kereket a kordé bal oldali kerékrendszere ω2 szögsebességgel, az e jelű fogaskereket pedig a jobb oldali kerékcsoport (-ω1) szögsebességgel hajtja. Azonos méretű fogaskerekek esetén a g és g'jelű fogaskerekek középpontjai
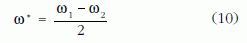
szögsebességgel keringenek az f és e kerekek tengelyei körül. (9) és (10) összevetéséből látható, hogy ha a kordé kerekek 2ρ ?átmérője megegyezik a b nyomtávval, az ω*?szögsebességgel keringő tengelyhez kapcsolt h irányjelző éppen a jármű Ω ?pillanatnyi kanyarodási szögsebességével ellentétes mértékben fordul el. Ez azt jelenti, hogy - hacsak a kerekek nem csúsznak meg - bármilyen pályán is haladjon a jármű, a szobor mindig a jármű pillanatnyi kanyarodásával ellentétesen fordul, a jelző kar tehát mindvégig az indulásnál beállított irányba mutat.
Bár elemzésünket sík felületi mozgást feltételezve végeztük el, bizonyítható, hogy a kordét bármilyen felület bármely zárt görbéje mentén csúszásmentesen gördítve a szobor karja párhuzamos eltolást végez. A kordé használatával tehát elvileg vizsgálható a Gauss- Bonnet-tétel2, ennek azonban az a feltétele, hogy a b nyomtávolság sokkal kisebb legyen, mint a vizsgálandó felület bármely görbületi sugara. Másképp megfogalmazva: a kordé karakterisztikus méretskáláján a felület nem lehet túl görbült vagy "göcsörtös".
Ennek illusztrálására nézzünk egy egyszerű példát, amikor a kordé egy gömb szélességi köre mentén gurul, majd a továbbiakban elemezzük a mozgást az úgynevezett pszeudoszférán.
A differenciálmű által mozgatott szobor szögelfordulása a szekérvázhoz képest a mozgás T időtartama alatt
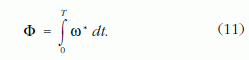
A kerekek szögelfordulásai a szekérvázhoz képest hasonlóképpen
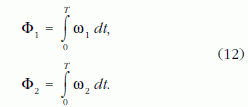
A kerekek csúszás nélkül legördült ívhosszai

Mivel
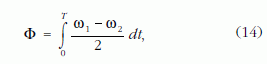
a szobor Φ ?szögelfordulása, valamint a kerekek által megtett S1 és S2 utak kapcsolata:

Gördüljön a kordé ω1 szögsebességgel forgó kereke az O középpontú, ismeretlen R sugarú gömb k1 körvonalán, az ω2 szögsebességgel forgó kerék pedig a k2 körvonalán (18. ábra).
Legyen AD = r1, BC = r2. A korábbiakkal összhangban CD = b = 2ρ ?a nyomtáv. A k2 kör sugara a geometriai viszonyokból (elemi trigonometriai azonosságokat alkalmazva) könnyen megkapható:
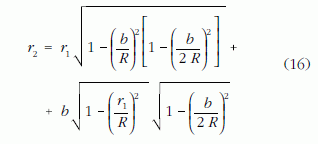
A kerekek által megtett utak az r1, illetve r2 sugarú körök kerületei:
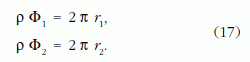
A (15)-(17) összefüggések alapján, a Maple R14 formulamanipulációs software alkalmazásával a
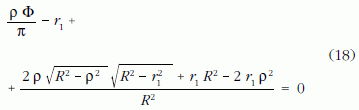
egyenlet adódik. A (18) egyenletet a gömb keresett R sugarára megoldva:
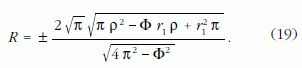
A 19. ábra a ρ?= 100 mm keréksugárhoz az r1 sugár és a Φ ?szög függvényében az R = állandó függvényeket szemlélteti.
Legyen a továbbiakban r = r1. A (20) formulából nyilvánvaló, hogy Φ → 2π ?esetén R → ∞, vagyis a síkon egy teljes kört megtevő kordé irányjelzője pontosan egy teljes körülfordulást végez. A kordé kerekeinek ρ sugarát - és egyúttal a b = 2ρ ?nyomtávot - 0-ra csökkentve a (19) határértéke:
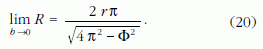
A (20) kifejezésből a szobor elfordulása a szekérvázhoz képest ekkor tehát
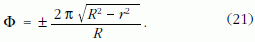
Az R sugarú gömbfelület r sugarú körvonala által határolt gömbsüveg felülete
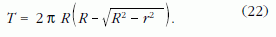
(21) és (22) összevetéséből látszik, hogy a b → 0 határesetben a kordé szobrának Φ ?szögű elfordulása valóban kimutatja a Gauss-Bonnet-tétel szerinti δ ?felületi excesszust:
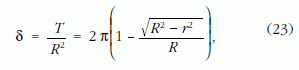
tehát

A 14.b ábrán szereplő kordéval az ELTE TTK Lágymányosi Campus központi épületének előcsarnokában álló földgömbön ellenőrző méréseket végeztünk (20. ábra).
A ρ ?= 103 mm kerék sugarú, b = 206 mm tengelytávú kordét a jó közelítéssel gömbnek tekinthető glóbuszon körbe gördítve,3 az irányjelző Φ ?= 285° ? szögelfordulása mellett az egyik kereke n = 7 1/3 körülfordulást végzett. A vizsgált kerék ekkor az
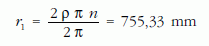
sugarú körön mozgott. A (19) formulát alkalmazva a gömb sugarára R ≈ ?1107 mm-t kaptunk. (Ellenőrzésül: a földgömb egyenlítői kerülete a modell talpán látható felirat szerint 6660 mm, ez alapján a glóbusz sugarára R* ≈ ?1060 mm adódik.)
A gömb mellett egy további állandó, K = -1 Gauss főgörbületű felület a pszeudoszféra. Az [1,0,0] ponton5 átmenő traktrix görbe z tengely körül forgatásával előállított pszeudoszféra (21. ábra) egyenlete:
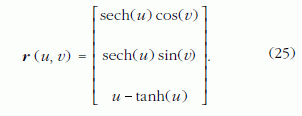
A pszeudoszféra első rendű Gauss-féle főmennyiségei a definiáló összefüggésekkel (ri a (25) vektor i-edik komponense):
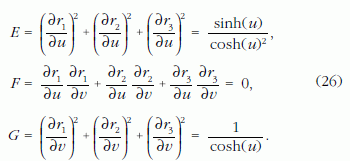
A pszeudoszféra felszíne az a ≤ u < ∞, 0 ≤ v ≤ ?2π ?határok között:
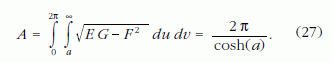
A Π1 jelű x-z koordináta-síkban (v = 0) a pszeudoszféra traktrix meridián görbéjének egyenlete:
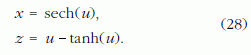
A traktrix görbületi sugara (az u változó szerinti deriválásokat vesszővel jelölve):
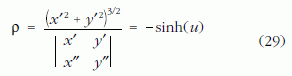
és a görbületi kör A középpontjának koordinátái:
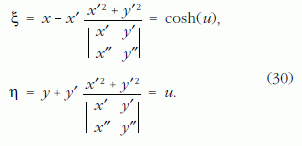
Mivel a pszeudoszféra forgásfelület, az y = 0 helyzetű P pontjához tartozó Π3 érintősík merőleges Π1-re. A Π1 és Π3 síkokra egyaránt merőleges Π2, a felület normálmetszeti síkja. Mivel a pszeudoszféra Gauss-görbülete K = –1, a Π2 síkmetszetben a görbületi sugár:
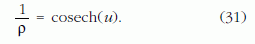
A geometriai viszonyokat a 22. ábrák szemléltetik. A 22.b ábra jelöléseivel
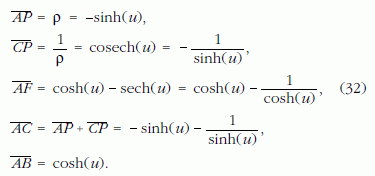
Az APF és ACB hasonló derékszögű háromszögek megfelelő oldalainak aránya:

A hiperbolikus függvények definíciói alapján nyilvánvaló, hogy
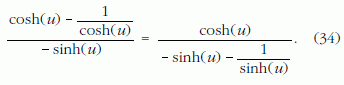
Azaz a Π2 síkmetszet görbületi körének C középpontja éppen a z tengelyre esik.
A P ponthoz tartozó parallel kör sugara (28) szerint, u = a helyettesítéssel
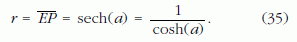
A 22.b ábra jelöléseivel a gömbre levezetett (23) összefüggés:
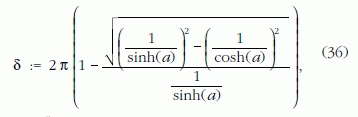
egyszerűsítve
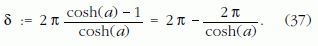
Ezzel a pszeudoszféra példáján is illusztráltuk a Gauss-Bonnet-tétel állítását.
A pszeudoszféra 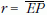 sugarú
parallel körén gördített
kordé mérési eredményei nyilván megegyeznek
a
sugarú
parallel körén gördített
kordé mérési eredményei nyilván megegyeznek
a 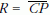 sugarú gömb r
sugarú parallel körén nyert
adatokkal.6 A gömbfelület és a pszeudoszféra lakói
azonban - ha csak erre az egy mérésre támaszkodnak
- a kordé alkalmazásával nem tudják világaik erősen
eltérő alakjait megkülönböztetni.
sugarú gömb r
sugarú parallel körén nyert
adatokkal.6 A gömbfelület és a pszeudoszféra lakói
azonban - ha csak erre az egy mérésre támaszkodnak
- a kordé alkalmazásával nem tudják világaik erősen
eltérő alakjait megkülönböztetni.
_______________________