Fizikai Szemle honlap |
Tartalomjegyzék |
Kovács Tamás
Max Planck Institute for the Physics of Complex Systems
Drezda, Németország
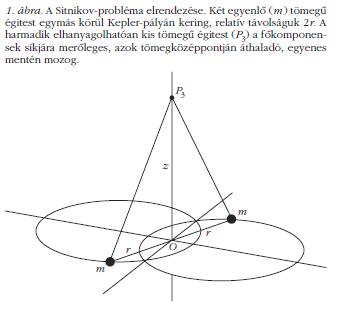
Nézzük meg először, hogy tényleg egyszerű-e? Egy tömegpontról akkor mondjuk, hogy Sitnikov-féle mozgást végez, ha egy egyenes mentén mozog, mégpedig olyan egyenes mentén, amely két egyenlő tömegű, egymás körül keringő égitest közös tömegközéppontján halad át. Itt mindjárt kiderül, hogy csillagászati példáról van szó. Amikor problémáról beszélünk, burkoltan a harmadik égitest mozgására vagyunk kíváncsiak, amit a két főkomponens (az egyenlő tömegű égitestek) gravitációs hatása befolyásol (1. ábra). A Newton-féle gravitációs erő centrális, azaz az adott tömegpontok között húzott egyenes mentén hat [1]. Ebből és a Sitnikov-rendszer szimmetrikus elrendezéséből következően a kis tömegű égitestre ható két erő eredője valóban a függőleges egyenesbe esik. Tehát a mozgás tényleg egy egyenes mentén zajlik. Ha a két főkomponens körpályán kering (azaz távolságuk minden időpillanatban állandó marad), akkor a harmadik égitestre - az egyenes bármely pontján - a fősíktól (a két nagy tömegű test keringési síkja) mért távolságával arányos erő hat. Ezen erő hatására a tesztrészecske (kis tömege miatt nevezhetjük így is) a tömegközéppont körül harmonikus rezgőmozgást végez.
Körpályát feltételezve a rendszer nem tűnik túlságosan bonyolultnak. Szép példája a középiskolai harmonikus oszcillátornak, bár a megoldás egy kicsit bonyolultabb alakú, ahogy azt már 1911-ben megmutatták [2].
Azonban nem véletlenül hivatkoznak problémaként a rendszerre. Ha megengedjük, hogy a főkomponensek keringjenek egymás körül, amit egy kettős csillagrendszer esetében joggal feltételezünk, és nem ragaszkodunk a görögök által tökéletesnek vélt körpályához, akkor a harmadik, kis tömegű égitest mozgásában drasztikus változásokat figyelhetünk meg. És ne gondoljunk arra, hogy nyolcas alakban vagy valami kusza pályán kezd el vándorolni. Mindvégig az egyenes mentén marad, de mozgása oly rendszertelenné válik, hogy azt a mai fizikában használatos kaotikus szóval illethetjük. És mindez csupán azért, mert a főkomponensek ellipszispályán keringenek egymás körül, vagy másképp megfogalmazva, időben változik a távolságuk, hol közelebb kerülnek egymáshoz (pericentrum környékén, ahogy a csillagászok mondják), hol pedig eltávolodnak egymástól (apocentrum környékén).
Még egy fontos következménnyel jár az, hogy gerjesztett rendszerrel van dolgunk. Nevezetesen, a harmadik test mechanikai energiája a mozgás során nem állandó. Az ilyen rendszerek dinamikai viselkedésével bővebben [3] foglalkozik. Ennyi ismerettel a hátunk mögött már nyugodtan mondhatjuk, hogy a Sitnikov-probléma valóban probléma. Hiszen vannak esetek, és ezek a tipikus esetek, amikor bizony bonyolult lehet az egyenes vonalú mozgás is. Természetesen ebben a bonyolultságban nyilvánul meg a rendszer dinamikai viselkedésének a szépsége, amelyet az írás következő részében ismerhet meg az Olvasó.
Mielőtt azonban a probléma alaposabb vizsgálatába fognánk, egy mondatot kell ejteni a rendszer névadójáról is. K. Sitnikov orosz matematikus volt, aki elsőként bizonyította az égi mechanika híres rendszeréről, a háromtest-problémáról, hogy benne oszcillátormozgás is lehetséges [4]. Ezért róla nevezték el ezt a speciális elrendezést.
Ha az ember kaotikus viselkedéssel találja szembe magát egy dinamikai rendszer vizsgálata során, értem itt ez alatt, ha a kitűzött feladat megoldása időben rendszertelen változást produkál, akkor néhány jól bevált módszert fel kell adni és helyettük újakat kell bevezetni. Itt három dolgot fogok röviden megemlíteni, amelyeket az Olvasó szinte minden, káosszal foglalkozó tankönyvben sokkal részletesebben is megtalál [3]:
 |
 |
A következőkben a fázistér alakzatainak megismerésén keresztül derítjük fel a probléma különböző mozgástípusait.
A rendszert leíró mozgásegyenletben egyetlen függő változó van, a harmadik égitest fősíktól mért távolsága, ezért mondhatjuk, hogy egy szabadsági fokú a rendszer. Ez részben igaz is akkor, amikor a kettősök körpályán keringenek, ha azonban a gerjesztés is megjelenik (ellipszisen mozog a kettős), akkor azt mondjuk, hogy másfél szabadsági fokú a rendszer. Az idő a plusz fél. Adott szabadsági fokú rendszer fázistere a szabadsági fokok számának kétszerese, mivel minden egyes szabadsági fokhoz tartozik egy helykoordináta és egy sebesség, amelyek a fázisteret kifeszítik. Ebből a szempontból az idő kicsit furcsa mennyiség, de a szabályhoz alkalmazkodik, úgyhogy a fél szabadsági foka egy fázistér-dimenziót ér. A Sitnikov- probléma fázistere tehát háromdimenziós, a kitérés, az ehhez tartozó sebesség és az idő, vagy a helyette bevezethető fázis, ami a főkomponensek pillanatnyi helyzetére jellemző. E három adat egyértelműen jellemzi a rendszer állapotát. Vagyis a mozgásegyenlet megoldása adott pillanatban ebben a 3-dimenziós térben egyetlen pont, követve a mozgást pedig egy folytonos fázisgörbe (trajektória).
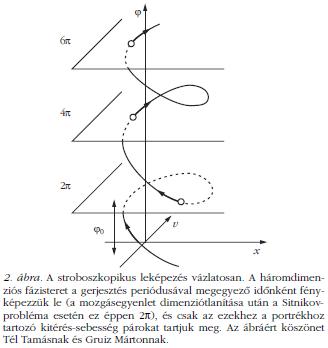
A kaotikus viselkedés tanulmányozásához, ahogy már említettem, leképezéseket célszerű bevezetni. Gerjesztett rendszerek esetén ez viszonylag egyszerű, mert csak a gerjesztés periódusát kell a mintavétel egységének választani, és így információvesztés nélkül kaphatunk képet a dinamikai viselkedésről. A Sitnikov-probléma esetében ez a háromdimenziós fázistér "feldarabolását" jelenti az időtengely (vagy a fázistengely) mentén. Az effajta leképezést stroboszkopikus leképezésnek nevezik, hiszen adott idő elteltével nézünk csak rá a rendszerre, és mentjük el a kitérés-sebesség (z, v) adatpárokat (2. ábra). Az elnevezést a hasonló elven működő stroboszkóplámpa ihlette.
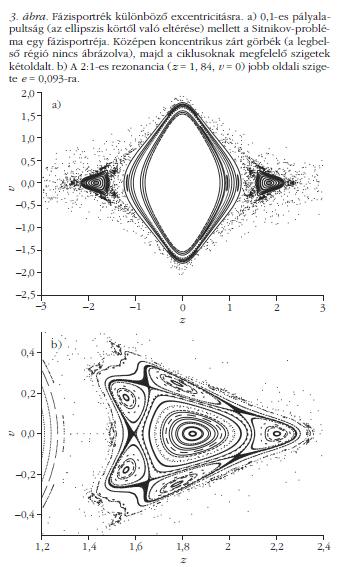
Most nézzük meg, hogy milyen szerkezetű egy ilyen stroboszkopikus metszet, fázisportré (3. ábra). Láthatunk rajta önmagukba záródó közel koncentrikus görbéket (amelyek "szigeteket" alkotnak), azok közepén elhelyezkedő pontokat, a görbék között vastag sötét sávokat, valamint szétszórt rendezetlenül elhelyezkedő pontokat. A következőkben azt ismerjük meg, hogy milyen mozgást reprezentálnak ezek az alakzatok.
 |
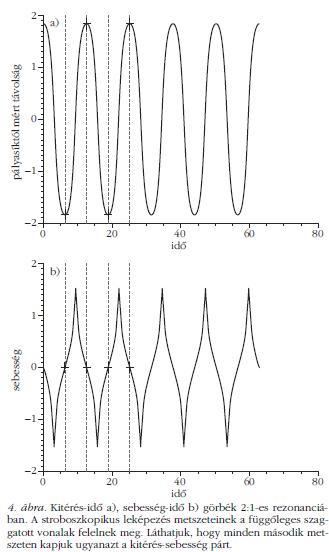 |
Haladjunk belülről kifelé. A zárt görbék minden esetben egy pontot fognak közre a fázistérképen. Ezek a pontok a periodikus mozgásoknak felelnek meg. Ez az a mozgástípus, mely során a harmadik égitest éppen ugyanabba a pozícióba, ugyanakkora sebességgel érkezik vissza minden egyes fénykép készítésekor (hasonlóan, mint az ingaóra ingája). Helyesebben szólva ez a megfogalmazás csak egyetlen pontra érvényes. Vannak olyan periodikus pályák, amelyek minden második fényképen lesznek ugyanazon a helyen, vagyis az 1., 3., 5. stb. fényképeken egy adott helyen jelennek meg, a páros számúakon pedig egy másik helyen. Az ilyen periodikus mozgásoknak két pont felel meg a fázisportrén, ahogy az látszik is a fő sziget két oldalán jobbról és balról nagyjából z = ±1,84 és v = 0 helyeken. Az, hogy ez a mozgás két pontot ad a metszeten azt jelenti, hogy amíg ugyanabba a pozícióba ugyanazzal a sebességgel megérkezik a részecske két fényképezés történik, azaz a főkomponensek két keringést végeznek. Az első keringés végén a tesztrészecske a z = -1,84, v = 0 pontban található, a második végén pedig a z = 1,84, v = 0 pontban. Az effajta mozgást kettes ciklusnak, vagy a csillagászatban használt 2:1-es rezonanciának mondjuk, mivel a tesztrészecske és a főkomponensek periódusideje racionális arányban állnak egymással. Így már kitalálható, hogy az egyetlen pont az 1:1-es rezonanciának felel meg, ahol a tesztrészecske - ahogy azt már láttuk - egy főkomponens-keringés alatt tesz meg egy teljes periódust. A harmadik égitest kitérésidő diagramján mindezt ellenőrizhetjük is (4. ábra ). A mozgás kezdőfeltételétől függően, ezeken kívül természetesen még számtalan különböző rezonancia található [5].
A következő mozgástípus nem annyira szabályos, mint az előző részben bemutatott tökéletesen periodikus. Ezek a pályák a fázisportrén zárt görbéket rajzolnak ki. Ez annak felel meg, hogy mozgása során a harmadik test a tömegközéppont körüli kitéréseket végez ugyan, de soha, egyik fényképezéskor sem tér vissza ugyanabba a pontba, ugyanazzal a sebességgel. Másképp mondva, a mozgás több periodikus megoldás összege, ilyenkor a főkomponensek keringési periódusa és a tesztrészecske periódusa nem racionális arányban állnak egymással. Az ilyen mozgásokat közel-periodikusnak, vagy idegen szóval kváziperiodikusnak mondjuk. Az elnevezésben benne van, hogy a mozgás viszonylag rendezett, de nem tökéletesen ismétli önmagát. Az, hogy közel-periodikus egy mozgás a fázisportrén - többek között - abban nyilvánul meg, hogy az általuk formált zárt görbék éppen a periodikus pályákat reprezentáló pontok körül alakulnak ki.
Bár a harmadik test energiája nem marad meg a mozgás során, általánosabb értelemben a dinamika mégis konzervatív, ugyanis a súrlódás hiánya miatt a fázistérfogat nem változik, konzerválódik (lásd Liouville-tétel). Ezért soroljuk a Sitnikov-problémát is a konzervatív rendszerek közé. Az 1960-as években kimondott és bizonyított matematikai tétel határozza meg, hogy a konzervatív rendszerekben a fázisportré zárt görbéi közül melyek maradnak meg hosszú ideig, és melyek azok, amelyek a rendszert érő zavaró hatás (jelen esetben a kettősök pályalapultsága) következtében felbomlanak, és "törmelékként" vastag sávokat hagynak maguk után [3, 6-8]. Ezekben a sávokban a mozgás időben rendezetlen, azaz a fényképezés pillanatában a sávon belülre majdnem bárhova eshet a pont. Ez a fajta mozgás tehát még "tökéletlenebb", mint a közel-periodikus megoldások voltak. Ezek a mozgások a kaotikus viselkedés megtestesítői a rendszerben. A kis tömegű égitest véges térrészben maradva végez rendezetlen mozgást, azaz a tömegközéppont-átmenetek rendezetlenül követik egymást. Az effajta mozgás érdekessége, hogy mindvégig (permanensen) kaotikus marad, és a részecske a tömegközéppont körül végtelen hosszú ideig, szabálytalan időközökkel oszcillál. Ez annak következménye, hogy a fázisportrén a görbék nem metszhetik egymást, ellenkező esetben a megoldás nem egyértelmű. Tehát a kaotikus sávokból a pontok nem vándorolhatnak el a fázis- tér tetszőleges területeire, mert ahhoz keresztezniük kellene az őket körülvevő közel-periodikus mozgásoknak megfelelő zárt görbéket (lásd 3.b ábra). Következésképpen a tesztrészecske a főkomponensek síkjától lefelé és felfelé csak meghatározott határok között mozoghat.
Fentebb említettem, hogy a kaotikus mozgás során a trajektória majdnem bárhová eljuthat a fázistér egy meghatározott részében. A majdnem szó annak köszönhető a mondatban, hogy ha nagyító alá tesszük ezeket a sávokat, láthatjuk, hogy kisebb skálán is jelen vannak a kváziperiodikus mozgás szigetei, mintegy beágyazva a kaotikus sávokba (5. ábra), és ez, bármekkora nagyítót is használunk, megmarad. Azt mondjuk, hogy a kaotikus sávok önhasonló alakzatok, nagyságrendekkel változtatva a felbontást ugyanazt a struktúrát kapjuk. Hasonlóan a szigetek partvonalához, a Hold felszínének kráterezettségéhez, vagy éppen a karfiol mintázatához. Az ilyen alakzatokat fraktáloknak nevezzük [9, 10].
Látható tehát, hogy a kaotikus viselkedés megjelenésével a fázistérben meghatározott alakzatok rajzolódnak ki. Kvantitatív vizsgálatok kimutatták, hogy a dinamika és a geometria rendezetlen mozgás esetén is szoros kapcsolatban áll egymással.
Itt mutatkozik meg a kaotikus viselkedés tanulmányozásában a fázistér használatának előnye, mert - ahogy láthatjuk - a rendezett mozgás egyszerű fázistérbeli megnyilvánulásai mellett a bonyolult viselkedésnek komplex, de jól meghatározható alakzatok felelnek meg.
A fázisportré szerkezetének kialakításában látszólag jelentéktelen szereplőnek tűnnek a szigetek között és körül - soha nem belül - elhelyezkedő rendezetlenül szétszórt pontok (3.a és 3.b ábra). Ha az Olvasó tüzetesebben megnézi az ábrákat, akkor láthatja, hogy a zárt görbék között nincsenek ilyen pontok. Ott a kaotikusan viselkedő pályák véletlenszerű pontjai a kaotikus sávot rajzolják ki, amelynek jól meghatározott szerkezete van, mint azt feljebb láttuk. Akkor vajon milyen mozgásnak felelnek meg a szétszórt pontok?
A korábbiakban már megismert kaotikus viselkedés, bármeddig is figyeljük a rendszert, mindvégig ugyanazt a fajta viselkedést mutatja. A permanens káosz jelenségével a fizikusok már a múlt század derekán tisztában voltak, az 1980-as évek közepétől azonban egyre inkább előtérbe került a kaotikus viselkedés azon fajtája, amely csak véges ideig tart, majd a kezdeti rendezetlenség után viszonylag egyszerű mozgásba "torkollik". Ezt a jelenséget véges idejű vagy másképpen tranziens káosznak nevezik. Eleinte disszipatív rendszerekben kutatták a jelenséget, mivel azok fázisterében találhatók olyan alakzatok, amelyek mintegy vonzzák a trajektóriákat, és miközben a fázisgörbék megközelítik ezeket az objektumokat, a mozgás kaotikus jelleget ölthet (miután elérték azokat, a bonyolult mozgás megszűnhet).
Vagyis, ha a rendszer időbeli viselkedését sokáig követjük, akkor a kezdetben rendszertelenül viselkedő mozgás rendezetté válhat.
Súrlódásmentes esetben is kimutatták a jelenséget. Ezekben a rendszerekben a véges idejű káosz szórási jelenségként realizálódik. Azaz a vizsgált részecske, tömegpont kezdetben szabályos mozgást végez, majd megközelíti a szórócentrumot, ott éri valamiféle fizikai hatás, majd e hatás következtében kidobódik, elhagyja a szórási tartományt, és mozgása ismét egyszerűvé válik. Itt a véges idejű kaotikus viselkedés a szórócentrum közelében figyelhető meg.
Nézzük példának a Sitnikov-problémát. Ebben, konzervatív rendszer lévén, várható szórási jelenség. Valahonnan "magasról" beejtjük a tesztrészecskét a tömegközéppont felé. Eleinte nagyon kis gyorsulással indul hiszen még elég távol van a főkomponensektől, és azok hatása így még igen kicsi. A tömegközéppont közelébe érve, ahol távolsága már összemérhető a kettős relatív távolságával, a főkomponensek gravitációs hatása egyre inkább érvényesül, és a harmadik égitest mozgása elveszti addigi (viszonylag egyszerű) jellegét. Elkezd oszcillálni a tömegközéppont körül, majd valamennyi idő múlva eltávolodik a fősíktól, és elhagyja a rendszert (felfelé vagy lefelé) ismét egyszerű mozgással.
A korábban említett szétszórt pontok a fázisportrén azoknak a "szóródó" pályáknak felelnek meg, amikor a részecske hosszabb-rövidebb idő után elhagyja a rendszert. Ahogy a végtelen idejű kaotikus viselkedésnek is egy meghatározott geometriájú alakzat, a kaotikus sáv felel meg a fázistérben, úgy a tranziens káoszért is egy jól definiálható objektum felel. Ezt nevezzük kaotikus nyereghalmaznak. Ennek egyik fontos tulajdonsága, hogy ez is fraktálhalmaz, akárcsak a kaotikus sávok. Geometriája azonban eltérő jellegű. Azt mondjuk, hogy a kaotikus nyereghalmaz kettős vagy összetett fraktál, mert mindkét irányban mérve, dimenziója tört szám. Természetesen ez is önhasonló, mint minden más fraktál (6. ábra). A tranziens jelenségek körében is megtalálták a kapcsolatot a mozgás dinamikai jellege, és a nyereghalmaz geometriai felépítése között. Itt kell megjegyezni, hogy ebben az összefüggésben szerepel egy eddig mellőzött, ám igen fontos tényező, a káosz átlagos élettartama. Ez, mint neve is mutatja, azt adja meg, hogy ha sok-sok különböző kezdőfeltételből induló mozgást vizsgálunk a nyereghalmaz közelében, akkor azok átlagosan mennyi ideig mutatnak - jelen problémánkban a fősík közelében - kaotikus viselkedést. Érdekes, hogy adott probléma, adott paraméterére ez az érték állandó bárhonnan is vesszük a kezdőfeltételeket.
Végezetül egy igen érdekes jelenséggel zárnám rövid kalandozásunkat a Sitnikov-probléma fázisterében. Említettem, hogy ha a numerikusan megszerkesztett nyereghalmaz (a 6. ábrán látható pontfelhő) valamely pontjából indítjuk a tesztrészecskét, akkor az megközelíti a tömegközéppontot, végez valahány, előre meghatározhatatlan számú rendszertelen rezgést, majd egyszercsak elhagyja a rendszert. Felmerül a kérdés, találhatunk-e olyan kezdőfeltételt, amelyből indítva a tesztrészecskét, az megközelíti a tömegközéppontot, és a továbbiakban mindörökké rendszertelen rezgéseket végez körülötte, azaz többé nem hagyja el a rendszert. A válasz, igen. E kezdőfeltételeknek "maga a nyereghalmaz" felel meg. A bökkenő csak az, hogy számítógéppel megtalálni nem lehet ezt az alakzatot, hiszen olyan végtelenül pontosan kellene választanunk a kezdőpontot, hogy arra a legtökéletesebb számítógép sem képes. Elméletileg tehát van kapcsolat a tranziens és permanens káosz között, gyakorlatilag azonban csak nagyon hosszú ideig "oda ragadó" mozgásokat mutathatunk ki számítógépes megoldásaink során.
Eddigiekben csillagászati problémáról volt szó. Felmerülhet a kérdés az Olvasóban, hol lehet megfigyelni ezt az égen? Sajnos a Sitnikov-probléma annyira speciális elrendezésű, hogy ehhez hasonló mozgás az általunk ismert csillagrendszerekben nem alakult ki. Gyakorlati jelentősége tehát itt véget is érhetne. Viszont egyszerűségének és a benne rejlő komplex dinamikai viselkedésnek köszönhetően számtalan káosszal foglalkozó könyv, dolgozat, közlemény tárgya volt már, amelyek során közelebb vitte mind a szerzőket, mind az olvasókat az egyszerű dinamikai rendszerekben megfigyelhető kaotikus viselkedés megértéséhez, továbbgondolásához. Jelen dolgozatnak is az a célja, hogy felkeltse az Olvasó érdeklődését a dinamikai rendszerekben megfigyelhető kaotikus viselkedés iránt.
_______________________________
Köszönet illeti Gruiz Mártont stilisztikai javaslataiért