Fizikai Szemle honlap |
Tartalomjegyzék |
Tél András, BME, Mechatronika alapszak, III. évfolyam
Tél Tamás, ELTE, Elméleti Fizikai Tanszék
A modern műszaki problémákban, így például a robotok tervezésekor gyakran lépnek fel irányítási, vezérlési feladatok. Ezek közül különösen érdekesek azok, amelyek során egy eredendően instabil állapotba kell eljuttatni a rendszert. Az alábbiakban bemutatunk egy első látásra reménytelennek tűnő mechanikai feladatot, amelynek megoldásához a modern fizika mára már klasszikussá vált eredményei adnak segítséget.
Tekintsünk egy egyenes mentén harmonikus rezgőmozgást végző m tömegű testet, amelynek rugóállandója egy előírt D(t) függvény szerint változik időben. Az x(t) kitérés-idő függvényt meghatározó mozgásegyenlet [1]
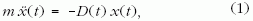
ahol a pont az idő szerinti deriválást jelöli. Az ennek az egyenletnek eleget tevő rendszer manapság érzékelők (szenzorok) és beavatkozó egységek (aktuátorok) segítségével könnyen megépíthető, bármilyen is a D(t) függvény. A rugóra ható erő most tehát nem csak a kitéréstől függ, hanem az időfüggő rugóállandó pillanatnyi értékétől is.1 Az (1) egyenlet jobb oldala expliciten is függ az időtől, a differenciálegyenlet nem autonóm, vagyis a mozgás folytatását nem csak a test pillanatnyi helyzete és sebessége határozza meg, hanem egy külső hatás is. Az egyenlet olyan típusú, mint a gerjesztett rezgéseket leíró egyenletek [1], csak az időfüggés nem egy külső erőben, hanem a rugóállandóban jelenik meg. A mechanikai összenergia a súrlódás hiányában sem állandó, hiszen a rugóállandó időbeli változása miatt a rendszer energiát nyerhet vagy veszíthet.
Tegyük föl ráadásul, hogy a rugóállandó időben monoton módon csökken, egy idő után előjelet vált, s attól kezdve végig negatív marad. Az egyszerűség kedvéért egységnyi tömeget tekintve, s alkalmasan megválasztott időegységet használva, ezt kifejezhetjük úgy is, hogy a mozgásegyenletet az
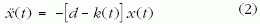
alakba írjuk. Itt d > 0 a nulla pillanathoz tartozó kezdeti rugóállandó, és k(t) az időbeli változást leíró rugófüggvény, amely nulláról indul és monoton módon tart a d-nél nagyobb A értékhez. Konkrétan válasszuk a k(t) rugófüggvényt
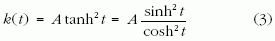
alakúnak, amely egy egyszerű, folytonos átváltást ír le 0 és A > d között. A rugófüggvény alakját és a d kezdeti értékhez való viszonyát az 1. ábra mutatja.
A (2) egyenlethez tartozó vezérlési probléma2 a következő: véges kezdeti kitéréssel indítva, adott A mellett, elérhető-e d alkalmas megválasztásával, hogy a test hosszú idő után megálljon?
Mivel a kezdeti rugóállandó az A nagyságú intervallumban változhat, ezt az intervallumot az operációs tartománynak nevezzük. Egy vezérlési feladat során az A értéket rögzítjük. A megoldás azért tűnik első ránézésre reménytelennek, mert az eredő rugóállandó egy idő után (t > tc -re) negatív, a rugó taszító, s a taszító rugók általános tulajdonsága, hogy egyre távolabbra juttatják a testet, amely formálisan tehát kifut a végtelenbe. A vezérlés lehetőségében azonban mégis reménykedhetünk, ha egy speciális feltétel teljesül. Ha a tc pillanatban a test nem távolodik az origótól, hanem közeledik hozzá, méghozzá elegendően nagy sebeséggel, akkor előfordulhat, hogy tehetetlensége miatt ezt a közeledést megtartja, s ámbár az eredő rugóállandó abszolútértéke nő, az eredő erő nagysága,
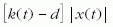
csökkenhet, ha ¦x(t)¦ elegendően kicsi és megfelelő ütemben csökken. Így tehát egészen kivételes esetekben, bizonyos d értékek mellett, lehetséges az, hogy a test hosszú idő után az origóhoz tartson, megálljon.
A speciális d értékek megtalálásához általában csak numerikus módszerekkel juthatunk. Rögzítsük ezért először a kezdőfeltételt oly módon, hogy a mozgás mindig egységnyi kitéréssel indul, kezdősebesség nélkül:
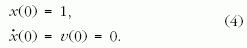
Az, hogy a kezdeti kitérés egységnyi, nem jelent megszorítást, mert a hosszegység szabadon választható (más szóval, azt a távolságot tekintjük hosszegységnek, amelyből a test indul). A vezérlés ezek után egyetlen mennyiség, a d kezdeti rugóállandó megválasztásával végezhető el. A mozgás numerikus integrálásához a Newton-egyenlet szimulálására jól bevált negyedrendű Runge-Kutta-módszert [2] választottuk, rögzített h lépésközzel. A negyedrendű jelző arra utal, hogy egy iterációs lépés h4 értékig pontos (a hiba nagyságrendje h5). Ez elegendő pontosságot biztosít, viszonylag rövid futási időkkel, a h = 0,01 választással. Mivel nagyobb d értékek mellett a kritikus tc idő nagyobb, a test hosszabb ideig rezeg, érdemes az A-hoz közeli d értékek vizsgálatával kezdeni.
Az A = 56, 55 < d < 56 választás mellett a kritikus pillanathoz körülbelül másfél rezgés után érünk el (a frekvencia közben lassan csökken, hiszen a [d-k (t)] rugóállandó is csökken). Ekkor d < 55,5-re, a kitérés negatív, a sebesség pozitív, de annyira nagy, hogy a test a negatív rugóerő ellenére jelentős sebességgel halad át az origón, s attól kezdve gyorsulva fut a végtelenbe (2. ábra). A d = 55 érték felé közeledve ez a kifutás egyre lassul. d = 55,0001 mellett az x(t ) függvény már közelít a t-tengelyhez, de kis szög alatt átmetszi. A d = 55 értékre a görbe numerikus pontossággal belesimul a t -tengelybe, amint a 2. ábrán is láthatjuk. Ekkor tehát sikeres a vezérlés! Az, hogy az ilyen d értékek mennyire kivételesek, jól látszik abból is, hogy d = 54,9999 és d = 54,99-ra a kitérés a negatív végtelenbe tart. A tc értéknél fellépő sebesség ekkor már nem elég ahhoz, hogy a test a negatív irányból eljusson az origóig, s miután azt megközelítve visszafordul, a taszító rugó egyre messzebbre távolítja.
Ez a tapasztalat jól mutatja, hogy az origó erősen instabil állapot. Vizsgálatára érdemes használni a dinamikai rendszerek módszertanából ismert eszközöket [3]. Tekintsük előszöris a (2) mozgásegyenlet hosszú idő elteltével érvényes alakját. Mivel t → ∞-re k(t) az A konstans értékhez tart, az egyenlet jobb oldalán (A-d)x áll. Mivel A > d, a zárójel pozitív, érdemes ezt s2-ként jelölni:

Az s mennyiség a taszítási paraméter. A mozgásegyenlet ezzel a rövidített jelöléssel

alakú, és egy időben konstans állandójú taszító rugó hatását írja le. Hosszú idő elteltével a kitérés általában nagy. A sikeres vezérléshez közeli esetekben azonban a (6) egyenlet érvényes ¦x¦ << 1 esetén is. Tegyük fel, hogy ilyen esettel van dolgunk, s indítsuk újra az időszámítást akkor, amikor a test már egy kis x0 koordinátájú és kis v0 sebességű állapotba került. Célunk ezzel annak megértése, hogy milyen a mozgás az origó környékén.
Vegyük észre, hogy a (6) egyenlet autonóm, ráadásul (éppen ezért) megoldható analitikusan. Mint minden lineáris, állandó együtthatós, homogén differenciálegyenletnek, megoldása kereshető exponenciális alakban. Az x = exp(λt ) feltevéssel a λ = ±s megszorításra jutunk, vagyis a λ kitevő csak a taszítási paraméter, s, vagy annak ellentettje, -s lehet. Az általános megoldás ezen alapmegoldások lineáris kombinációja. Könnyen ellenőrizhető, hogy a (6) egyenlet x(0) = x0, v (0) = v0 kezdőfeltételt kielégítő megoldása
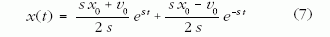
alakú. A megoldás tehát két exponenciális összege, amelyek közül egy idő után a pozitív kitevőjű, exp(s t) tag válik dominánssá. Ez írja le a végtelenhez tartást. Mindez azonban csak akkor igaz, ha az sx0+v0 együttható nem nulla. Bizonyos kezdőfeltételekre azonban fennállhat, hogy sx0+v0 = 0, s ekkor

Ilyenkor tehát a test egyre csökkenő sebességgel az origóhoz tart. Ennek az esetnek kell tehát megvalósulnia sikeres vezérlés esetén.
Az origó körüli viselkedésről áttekintő képet a fázistérben kaphatunk, ahol a v = x sebességet ábrázoljuk az x kitérés függvényében. Fenti eredményünk azt mutatja, hogy a

egyenes mentén elhelyezkedő pontok éppen eljutnak az origóba, ha ¦x¦ << 1. Vagyis, ha jól meghatározott sebeséggel lökjük az instabil állapot felé a testet, akkor az megáll. A nulla sebesség elérése elvileg végtelen hosszú ideig tart, de gyakorlatilag az 1/s idő néhányszorosa után a test már nagyon jó közelítéssel megközelíti a nyugalmi állapotot. Az egyenesen kívüli kezdőfeltételek mind a végtelenbe vezetnek. A v = sx egyenes mentén levő pontoknak megvan az a sajátos tulajdonsága, hogy esetükben sx0-v0 = 0, és ők egyetlen exponenciálisan növekvő függvény szerint távolodnak, x(t) = x0est.
A fázistér v = -sx egyenese a fentiek szerint azt a speciális mozgást írja le, amely az origóba történő eljutásnak felel meg. Ezt a görbét ezért az origó stabil görbéjének, a dinamikai rendszerek szóhasználatával stabil sokaságának [3] hívjuk. A v = sx egyenes, amelynek mentén az eltávolodás a leggyorsabb, az origó instabil sokasága. A 3. ábrán is látható, hogy a fázissíkot a stabil és instabil sokaságok négy síknegyedre osztják.
Általában is igaz [3], hogy a mechanikában előforduló minden autonóm rendszer instabil állapota ilyen típusú. A keresztalakzat megjelenése azt fejezi ki, hogy az instabilitás sohasem tökéletes. A fázistér egy elhanyagolhatóan csekély mértékű tartományából (a teljes sík egy vonalából) mindig el lehet jutni az instabil állapotba. (A hegyére állított ceruza állapotát instabilnak mondjuk, pedig kezdeti kitérítés esetén ott is találhatunk egy megfelelő kezdősebességet, amellyel meglökve az éppen megáll a függőleges helyzetben.) Az instabil állapotok tehát mindig nyeregpontok a fázistérben, olyan pontok, amelyekhez tartozik stabil és instabil sokaság.3
Számunkra a stabil sokaság bír különös jelentőséggel, hiszen a vezérlés csak ezen görbe mentén lehet sikeres. Örülhetünk annak, hogy alakját a (9) összefüggés szerint egzaktul ismerjük, de ez csak akkor igaz, ha a test már közel került az origóhoz. Mit mondhatunk az origótól távol eső pontok vezérlési esélyéről? A folytonosság miatt feltételezhetjük, hogy az origó stabil sokasága a teljes (2) egyenlet fázisterében is létezik. Ha tehát nem kötjük magunkat a t >> 1 feltételhez, az eredeti nem autonóm egyenlet fázisterében is találunk egy olyan görbét, amely hosszú idő után befut a (9) egyenesbe, s azon keresztül az origóba. Ezt a stabil sokaságot numerikusan kell megkeresni, s a kérdés az, hogy a (4) kezdőfeltétel adott d mellett ráesik-e az origó stabil sokaságára. Azon d értékek, amelyekre ez teljesül, a vezérlést biztosító d értékek. A 4. ábra mutatja, hogy d = 55 esetén az (1,0) pont valóban rajta van az origóba vezető stabil sokaságon. Autonóm rendszerekben a stabil sokaság nem metszheti önmagát. Mivel azonban rendszerünk nem autonóm, több metszéspontot is megfigyelhetünk. (Azt is mondhatjuk, hogy az igazi fázistér 3 dimenziós, amelyet x, v és a rugóállandóban megjelenő idő feszít ki, s mi az igazi, önmagát nem metsző sokaságnak az (x, v) síkra vett vetületét látjuk.)
Vizsgáljuk ezek után, létezik-e még másik, vezérlésre alkalmas d érték A = 56 mellett. Ezt numerikusan úgy tehetjük meg, hogy programot írunk, amely az összes d értéket megvizsgálja Δd = 0,01 lépésenként a 0 < d < A operációs tartományban. Minden egyes d-hez numerikusan meghatározza az x(t) függvényt, s rögzíti annak értékét egy késő időpontban (például t = 30-ban). A program, amely a LabView grafikus programnyelven íródott [4], újabb és újabb d értékeket vesz mindaddig, amíg azt nem érzékeli, hogy a későbbi időpontban felvett x érték előjele különbözik az előző d-hez tartozó előjelétől. Ekkor megáll és kiírja az utolsó d értéket, amelynek környékén léteznie kell egy vezérlést megvalósító értéknek, hiszen itt simul hozzá az x(t) függvény a t-tengelyhez (vagyis ugyanaz zajlik le, mint a 2. ábrán, csak más d-re).
Ezzel a módszerrel összesen még három vezérlésre alkalmas d értéket találunk, amelyek 7, 31, és 47. A kitérés-idő függvény ezekre rendre negyed, háromnegyed és ötnegyed rezgés után tart az origóba. A fázistérbeli képen ennek megfelelően az origó elérése előtti rajzolat egyre bonyolultabb, és egyre több metszéspont figyelhető meg (5. ábra ). Vegyük észre, hogy az alacsonyabb d értékekre az origó egyre instabilabb, az (5) taszítási paraméterre rendre a 7, 5 és 3 értékeket kapjuk. Ennek megfelelően a nyeregpontra jellemző keresztalakzat egyre meredekebb a fázissíkon.
Az A = 56 paraméter esetén tehát összesen négy vezérlést biztosító kezdeti rugóállandó értéket találtunk a (4) kezdőfeltétellel. Az ilyen típusú feladatok a sajátérték-problémák körébe tartoznak: megoldások csak bizonyos diszkrét dn = d0, d1, ..., dnmax értékek mellett találhatók.
Az A paraméter más értékei mellett is ugyanezt a jelleget látjuk. A tapasztalat az, hogy A növelésével nő a sajátértékek száma. Az 1. táblázatban összefoglaljuk néhány jellegzetes A paraméter mellett a talált dn sajátértékeket, a rugóállandó-spektrumokat.
A táblázatból több érdekes szabályosság olvasható ki. Adott A mellett az (n+1)-edik és az n-edik sajátérték különbsége például 8 egész számú többszöröse. Egyszerű összefüggésre jutunk, ha észrevesszük, hogy a vizsgált A értékek két egymás utáni egész szám szorzataként írhatók,

ahol λ > 1. Az adott λ-hoz tartozó első sajátérték min- A = λ (λ 1), (10) dig λ-1, és dn+1-dn = 4λ-8(n+1). Ezek után könnyen felismerhető az általános szabály:
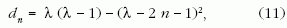
amely n = 0-tól a maximális nmax = [(λ-1)/2] értékig érvényes, ahol a szögletes zárójel az egész részt jelöli. A dn sajátértékhez tartozó (5) taszítási paraméter: sn = λ-2n-1, amiből látszik, hogy minél kisebb n, annál instabilabb a probléma. Mivel minden pozitív szám írható a (10) alakban, érthető és numerikusan is ellenőrizhető, hogy a (11) rugóállandó-spektrum tetszőleges valós λ-ra is érvényes.
Térjünk most át egy másik kérdéskörre, a kvantummechanikai energiasajátérték-problémára (a figyelmes Olvasó bizonyára már amúgyis észrevette a két feladat hasonlóságát). Mint ismert, az egydimenziós, sima V(x) potenciálban mozgó m tömegű részecske E energiáját a
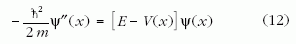
stacionárius Schrödinger-egyenlet határozza meg [5-7], ahol ħ a Planck-állandó és a vessző az x helykoordináta szerinti deriválást jelöli. A Ψ(x) hullámfüggvénynek folytonosan differenciálhatónak kell lennie, és kötött állapotban nagy távolságokban nullához kell tartania. Ez az egyenlet mikroszkopikus részecskékre vonatkozik, és időtől független. Hogyan vethető össze a (2) makroszkopikus vezérlési problémával, amely a klasszikus fizika Newton-egyenlete?
Az ilyen távoleső problémák közötti lehetséges kapcsolat felderítésében nélkülözhetetlen segítség az egyenletek dimenziótlanítása [3]. A módszer nagyon egyszerű, és sok más esetben (például egyenletek numerikus megoldásra alkalmas alakjának megtalálásában) is hasznos. Az alapgondolat az, hogy minden problémának megvan a saját jellegzetes hosszúság- vagy időskálája. A Schrödinger-egyenlet esetén ilyen jellegzetes skála lehet a potenciál jellemző mérete, például félszélessége. Tekintsük távolságegységnek ezt az a mikroszkopikus hosszat az SI-rendszer méter (vagy nanométer) egysége helyett. Ez formálisan azt jelenti, hogy elvégezzük az x; → ax transzformációt. Az új x változó a dimenziótlan helykoordináta, amely megadja, hogy a távolság hányszorosa a a hosszegységnek. A bonyolult jelölésváltás elkerülése érdekében jelöljük V(x), Ψ(x)-szel a potenciál- és a hullámfüggvény dimenziótlan helykoordinátával kifejezett alakját is. Ha ennek szellemében vesszővel kívánjuk jelölni a dimenziótlan x szerinti deriváltat is, akkor figyelembe kell venni, hogy minden egyes eredeti x szerinti deriválás egy a-val való osztást hoz be. Mivel kétszeres deriválásról van szó, a dimenziótlan helyváltozóban érvényes Schrödinger-egyenlet
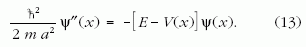
Most mindkét oldal energia mértékegységű. A bal
oldalon álló E* = ħ2/(2ma2) konstans tekinthető a
probléma jellegzetes energiaértékének. Ha a jobb
oldalon levő energiát és potenciált ebben az E* egységben
mérjük, akkor helyettük az
e = E/E*, 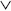 (x) = V(x)/E*
dimenziótlan energia- és dimenziótlan potenciálfüggvény
jelenik meg, és a
(x) = V(x)/E*
dimenziótlan energia- és dimenziótlan potenciálfüggvény
jelenik meg, és a
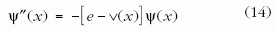
egyenletre jutunk. Az atomi méretekre jellemző a = 10-10 m-rel, m = 9 · 10-31 kg elektrontömeggel és a ħ = 10-34 Js Planck-állandóval számolva az energiaegység E* = 5 · 10-19 J ≈ 3 eV, ami valóban atomi kötésekre jellemző energiaérték. Az E összenergia ennek néhányszorosa, így a dimenziótlan egyenlet már nem függ az eredeti skáláktól, nem maradt benne semmilyen mikroszkopikus paraméter.
Ezen a ponton felismerhetjük, hogy a (14) dimenziótlan Schrödinger-egyenlet a már eddig is vizsgált (2) egyenlethez hasonló, sőt alakjuk az x↔ t csere után teljesen megegyezik!
Érdemes megjegyezni, hogy a vezérlés dimenziós (1) egyenletét, amelyet a D(t)= D-K(t) felbontással az
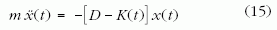
alakban írhatunk, hasonló eljárással hozhatjuk a (2) alakra. A rugóállandó időbeli változásának nyilván van egy jellegzetes ideje τ, amely lehet például az az idő, amely alatt a rugóállandó értéke a felére csökken. Az időt τ egységeiben mérve, a D* = m/τ2 rugóállandó-egységet kapjuk, amellyel (15)-ből (2)-re jutunk.4
A dimenziótlan egyenletek
ekvivalenciájának felismerése
után természetesen vizsgálnunk
kell a kezdeti és peremfeltételeket
is. A vezérlés feltételeként
megkövetelt x(t → ∞) = 0 megkötés
teljesen megfelel a hullámfüggvény
normálhatóságával
kapcsolatos Ψ(¦x¦ → ∞) = 0 peremfeltételnek.
A vezérlési probléma
kezdőfeltételének kvantummechanikai megfeleltetése
több figyelmet igényel. A Schrödinger-egyenlet a
teljes V(x) potenciált vizsgálja, s nem szorítkozik
annak csak a pozitív (x > 0) koordinátákhoz tartozó
felére. Páros potenciálfüggvények, azaz V(x) = V(-x)
esetén, a szimmetria miatt tudjuk, hogy létezniük kell
páros hullámfüggvényeknek, s ezek a függvények az
origóban vízszintes érintőjűek.Ők, az x ↔ t csere értelmében
pontosan megfelelnek a (4) mechanikai
kezdőfeltételnek. A páros sajátfüggvényekhez a teljes
en energiaspektrum páros n indexű értékei rendelhetők.
A páratlan indexű energiaértékek az origóban
eltűnő pontszimmetrikus hullámfüggvényekhez tartoznak.5 A két probléma közötti megfeleltetés tehát
az, hogy ha azonos alakú a dimenziótlan k (t) és 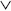 (x)
függvény, azaz, ha k (t) =
(x)
függvény, azaz, ha k (t) = 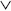 (x=t) és ha
(x=t) és ha
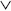 (x) páros,
akkor a dimenziótlan spektrumok megfelelnek egymásnak;
a (4) kezdőfeltételhez tartozó vezérlési probléma
dimenziótlan spektruma a
(x) páros,
akkor a dimenziótlan spektrumok megfelelnek egymásnak;
a (4) kezdőfeltételhez tartozó vezérlési probléma
dimenziótlan spektruma a

szabály szerint kapható meg az en dimenziótlan kvantummechanikai spektrumból. A példaként használt (3) függvénycsalád a kvantummechanikában a
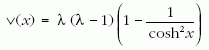
dimenziótlan potenciálnak felel meg, az úgynevezett Rosen-Morse-potenciálnak [7, 8].6
Még egyszerűbb példát kapunk a parabolikus k (t)
= t2 rugófüggvény, 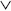 (x) = x2
dimenziótlan potenciál
esetén, amely a V(x) = 1/2mω2x2 harmonikus oszcillátor
problémának felel meg az
E* = ħω/2, a2 = ħ/(mω)
egységválasztással. A
rugóállandó-spektrum
az ismert [5, 6] lineáris En = ħω(n+1/2), en
= 2n+1
spektrumból következően dn = 4n+1 alakú.7
(x) = x2
dimenziótlan potenciál
esetén, amely a V(x) = 1/2mω2x2 harmonikus oszcillátor
problémának felel meg az
E* = ħω/2, a2 = ħ/(mω)
egységválasztással. A
rugóállandó-spektrum
az ismert [5, 6] lineáris En = ħω(n+1/2), en
= 2n+1
spektrumból következően dn = 4n+1 alakú.7
Sajnos, az egzaktul megoldható kvantummechanikai problémák száma csekély [6, 7], ezért csak nagyon ritkán számíthatunk arra, hogy a dn spektrum kifejezhető egyszerű képlettel. A vázolt numerikus eljárás azonban mindig célhoz vezet.
Feltehető az a kérdés is, hogy milyen kvantummechanikai
feladatot oldunk meg a k (t) függvény megválasztásával.
Mivel az idő pozitív, a potenciálnak
pedig negatív x koordinátákra is értelmezettnek kell
lennie, azt mondhatjuk, hogy 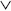 (x) = k(t=x), negatív
x-ekre pedig
(x) = k(t=x), negatív
x-ekre pedig 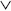 (x) =
(x) = 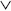 (-x).
Vagyis, a (4) kezdőfeltételnek
eleget tevő vezérlési feladat a k (t )-nak megfelelő
potenciál páros kiterjesztését tartalmazó energiasajátérték-
problémának felel meg, és abban is a páros
sajátértékeket adja meg dn. Így a dn -hez tartozó vezérelt
x(t) kitérés-idő függvény páros kiterjesztése a t → x
helyettesítés után a
(-x).
Vagyis, a (4) kezdőfeltételnek
eleget tevő vezérlési feladat a k (t )-nak megfelelő
potenciál páros kiterjesztését tartalmazó energiasajátérték-
problémának felel meg, és abban is a páros
sajátértékeket adja meg dn. Így a dn -hez tartozó vezérelt
x(t) kitérés-idő függvény páros kiterjesztése a t → x
helyettesítés után a 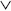 (x) potenciál 2n-edik sajátállapotához
tartozó hullámfüggvényt adja meg (6. ábra).
(x) potenciál 2n-edik sajátállapotához
tartozó hullámfüggvényt adja meg (6. ábra).
A tc kritikus idő megfelelője az xc kritikus távolság. Ez az a helykoordináta, ahol az összenergia megegyezik a potenciális energiával, vagyis, ahol a klasszikus fizika törvényeinek eleget tevő részecske visszafordulna. Az, hogy a kvantummechanikai feladatban a részecske véges valószínűséggel lehet az xc-nél nagyobb távolságban is, az alagúteffektus jelensége. Éppen ez az a tartomány, ahol a vezérlési feladatban a rugóállandó negatív! A vezérlési és a kvantummechanikai probléma megfeleltetésének legfontosabb gondolatait foglalja össze a 2. táblázat.
Vizsgáljuk most meg, hogyan alakul a vezérlési feladat, ha az x(0) = 1 helyzetből nullától eltérő v0 ≠ 0 kezdősebességgel indítjuk a testet. A v0 = 1 értékkel A = 56-ra a numerikus megoldást követve azt tapasztaljuk, hogy d = 7 körül nem sikeres a vezérlés, de d = 9,526-ra sikeressé válik. Ez szemléletesen is érthető, hiszen, ha a test kezdetben határozottan távolodik az origótól, akkor a kritikus idő (amely független v0-tól) eltelte után még viszonylag messze van az origótól, így a taszító erő d = 7 körül még kiveti a pozitív végtelenbe. Az origó pozitív irányból való lassú elérése csak valamelyik nagyobb d értéknél válik lehetővé. A 7. ábrán a kitérés-idő függvényen kívül a fázistérbeli rajzolatot is láthatjuk, amely topológiailag azonos a d = 7, v0 = 0 értékhez tartozóval (5.a ábra). Az (1, v0) kezdőpont természetesen rajta van az origó stabil sokaságán, ha d = 9,526.
Ez a megfigyelés azt sugallja. hogy minden egyes v0 dimenziótlan sebességhez tartozhat egy dn (v0) rugóállandó- spektrum. A numerikus tapasztalat ezt alátámasztja, amint azt a 3. táblázat néhány esetre bemutatja.
Az a szabály olvasható le, hogy pozitív kezdősebességek az eredeti sajátértékeket növelik, a negatívak csökkentik. Különösen érdekes a v0 = -2 eset, amikor nem találunk sajátértéket a 0 < d < 7 tartományban. A kezdősebesség ekkor olyan nagy negatív szám már, hogy a pozitív értékek felől oszcillálás nélkül az origóba tartó megoldás már nem is létezhet. Nagyobb n-ekre a kezdősebesség hatása egyre kisebb, a függvények egyre később csengenek le, és rájuk a kezdeti meredekség-változás kisebb hatással van.
A vezérlési és a kvantummechanikai probléma fenti
összehasonlítása alapján felmerül a kérdés: mondhatjuk
ezek után, hogy a v0 ≠ 0 esetekkel a 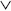 (x) = k(t=x)
potenciál
újabb kvantummechnikai sajátértékeket fedeztünk
fel? Semmiképpen sem! A vezérlés véges meredekséggel
induló x(t) függvényének x tengelyre vett
tükrözésével kapott páros kiterjesztése ugyanis megtörik
az origóban. Ez nem feleltethető meg kvantummechanikai
hullámfüggvények, hiszen Ψ-nek differenciálhatónak
kell lennie (különben például nem lenne egyértelműen
értelmezhető rá az impulzusoperátor: a deriválási
operátor hatása). A levonható konklúzió az, hogy
a vezérlési probléma bővebb, mint a kvantummechanikai,8
mert több megoldása létezik, mint a kvantummechanikainak,
hiszen minden v0 értékhez (nem csak v0 = 0-hoz) tartozhat
egy rugóállandó-spektrum. Ennek oka,
hogy a klasszikus x(t ) függvényre kevesebb megszorítás
létezik, mint a hullámfüggvényre. Ugyanakkor
azonban a vezérlési probléma minden egyes v0-nál
ugyanolyan (akár analitikus) módszerekkel oldandó
meg, mint a Schrödinger-egyenlet.
(x) = k(t=x)
potenciál
újabb kvantummechnikai sajátértékeket fedeztünk
fel? Semmiképpen sem! A vezérlés véges meredekséggel
induló x(t) függvényének x tengelyre vett
tükrözésével kapott páros kiterjesztése ugyanis megtörik
az origóban. Ez nem feleltethető meg kvantummechanikai
hullámfüggvények, hiszen Ψ-nek differenciálhatónak
kell lennie (különben például nem lenne egyértelműen
értelmezhető rá az impulzusoperátor: a deriválási
operátor hatása). A levonható konklúzió az, hogy
a vezérlési probléma bővebb, mint a kvantummechanikai,8
mert több megoldása létezik, mint a kvantummechanikainak,
hiszen minden v0 értékhez (nem csak v0 = 0-hoz) tartozhat
egy rugóállandó-spektrum. Ennek oka,
hogy a klasszikus x(t ) függvényre kevesebb megszorítás
létezik, mint a hullámfüggvényre. Ugyanakkor
azonban a vezérlési probléma minden egyes v0-nál
ugyanolyan (akár analitikus) módszerekkel oldandó
meg, mint a Schrödinger-egyenlet.
Annak más oldalról történő megvilágítására, hogy a
kvantummechanikai probléma megoldása bonyolultabb,
több megkötésnek tesz eleget, mint a mechanikai,
érdemes röviden kitérni az általános, azaz nem
páros, egyetlen minimumú 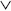 (x) potenciál esetére. Válasszuk
az origót a potenciál minimumának. A pozitív
és a negatív x értékekhez tartozó potenciálból pozitív
időkre két különböző rugófüggvény definiálható k1(t) =
(x) potenciál esetére. Válasszuk
az origót a potenciál minimumának. A pozitív
és a negatív x értékekhez tartozó potenciálból pozitív
időkre két különböző rugófüggvény definiálható k1(t) =
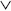 (t=x>0) és k2(t) =
(t=x>0) és k2(t) =
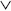 (t=-x>0). Mivel a hullámfüggvénynek
mind a pozitív, mind a negatív végtelenben el kell
tűnnie, a megfelelő vezérlési feladatban két különböző
differenciálegyenletet kell megoldanunk, mindkettőt
pozitív időkre, s ugyanazzal a d-vel:
(t=-x>0). Mivel a hullámfüggvénynek
mind a pozitív, mind a negatív végtelenben el kell
tűnnie, a megfelelő vezérlési feladatban két különböző
differenciálegyenletet kell megoldanunk, mindkettőt
pozitív időkre, s ugyanazzal a d-vel:
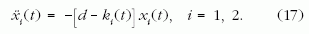
A kezdőfeltétel az, hogy az 1-es esetben x1(0) = 1, v1(0) = v0, a másik esetben viszont x2(0) = 1, v2(0) = -v0, ugyanis az x2 megoldás x-tengelyre való tükrözésével kapott teljes megoldás: Ψ(x>0) = x1(t=x), Ψ(x<0) = x2(t=-x) csak így lehet folytonosan deriválható az origóban. Az energiaspektrum megtalálása azt jelenti, hogy minden egyes véges v0 és d mellett végig kell próbálnunk, hogy vezérelhető-e mindkét feladat egyszerre.
Megmutattuk, hogy létezik egy időfüggő vezérlési feladat, amely szoros hasonlóságot mutat az egydimenziós kvantummechanikai energiasajátérték-problémával, amennyiben a helykoordinátában páros potenciálokat vizsgálunk. Még ekkor is, a vezérlési feladatnak jóval több diszkrét megoldása létezik, mint a kvantummechanikainak, mert a vezérelt részecskének lehet kezdősebessége is. A sikeres vezérlés mindig egy instabil pont (az origó) elérését jelenti, ami csakis a stabil sokaság mentén lehetséges. A vezérlés feltétele tehát úgy fogalmazható meg, hogy a kezdőfeltétel essen rá az origó stabil sokaságára. A dinamikai rendszerek szemlélete új megvilágításba helyezi a klasszikus kvantummechanikai energiasajátérték-problémát is.
Köszönetnyilvánítás
Köszönjük Varga Balázs tanár úrnak (Eötvös József Gimnázium, Budapest), hogy olyan modern fizikai órákat tartott, amelyek alapján a 11-edikes diákban felmerült a kérdés: mi lehet a Schrödinger-egyenlet időbeli megfelelője. Ez vezetett el a bemutatott gondolatmenethez.
_________________________
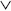 (x) = λ2x2,
ahol λ > 0 tetszőleges szám, akkor az
E* = ħω/(2λ), a2 = ħλ/(mω) választással az
en = (2n+1)λ dimenziótlan
spektrumra jutunk, amelyből dn = (4n+1)λ. Ugyanez következik
(11)-ből is a nagy λ határesetben, véges n-ekre. Ennek oka az,
hogy a (3) rugófüggvény parabolikusan indul: k(t) = λ(λ-1)t2, és
nagy λ-ra λ(λ-1) ≈ λ2.
(x) = λ2x2,
ahol λ > 0 tetszőleges szám, akkor az
E* = ħω/(2λ), a2 = ħλ/(mω) választással az
en = (2n+1)λ dimenziótlan
spektrumra jutunk, amelyből dn = (4n+1)λ. Ugyanez következik
(11)-ből is a nagy λ határesetben, véges n-ekre. Ennek oka az,
hogy a (3) rugófüggvény parabolikusan indul: k(t) = λ(λ-1)t2, és
nagy λ-ra λ(λ-1) ≈ λ2.