Fizikai Szemle honlap |
Tartalomjegyzék |
Patkós András
ELTE, Atomfizikai Tanszék
A konsztituens kvarkok végső áttörését a nehéz kvarkok felfedezése hozta meg. A J /Ψ 3,096 GeV/c2 tömegű, igen keskeny szélességű (Γ = 93 keV/c2) rezonancia felfedezését két független kísérleti elrendezés méréseire alapozva 1974. november 11-én jelentették be. A hosszú élettartam értelmezésére természetesen kínálkozott Zweig egykori gondolatmenetének megismétlése, azaz egy újfajta kvark-antikvark párból álló szerkezet feltételezése. A bájos c kvark és antikvarkja kötött állapotainak 1976 végére felfedezett sorozata e kvarkok létezését ugyanúgy alátámasztotta, amint az atomi spektroszkópia szolgál az atomok összetett szerkezetének legfontosabb bizonyítékául.
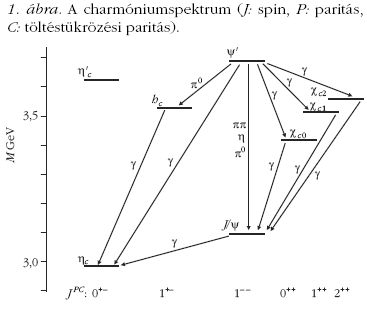
A proton-proton ütközésben keltett e+e- pár invariáns tömegében megjelenő rezonanciacsúcs, amelyet S. Ting csoportja talált Brookhavenben, egyben magyarázatot adott a korábban µ+µ- pár megfigyelésével kapott "váll" kialakulására, amit az ismert kvarkokra épülő partonmodell, immár érthető módon, nem tudott kielégítően megmagyarázni. Ez a technika azonban finomabb vizsgálatra nem volt alkalmas. Az igazi áttörést a stanfordi SPEAR elektron-pozitron tárológyűrűben bekövetkező szétsugárzási folyamatban felfedezett első rezonancia feletti tartomány finom lépésekben végrehajtott "letapogatása" hozta, amelyet az 1976-os Nobel-díj másik jutalmazottja, B. Richter vezetett. Az annihilációban kialakuló instabil elektromágneses térből életrekelt 1- - spin-paritású (JPC) hadronállapotoknak és az azokból foton kisugárzásával létrejövő további, pozitív paritásúaknak az 1. ábrán bemutatott spektroszkópiai vonalrendszere világos párhuzamot mutat az atomfizikai leírással jól modellezhető pozitróniumspektrummal. A spektrum elméleti értelmezése során bekövetkezett az a kivételes helyzet, amikor a nem-relativisztikus Schrödingeregyenlet megoldásából származó, szinte egyetemi gyakorlószintű spektrumszámolásokat a Physical Review Letters azonnal elfogadta közlésre.
A nagyjából 1,6 GeV/c2 tömegű összetevők között ható Coulomb-szerű potenciál mellé (amelyben az összetevők elektromos töltése helyére azzal analóg erős "töltést" írtak a szerzők) a kvarkok kiszabadulását megakadályozó, a távolsággal lineárisan növekvő potenciális energiát eredményező tagot és a kettőt összesimító állandót adtak. E három paraméter illesztésével végrehajtott számítások nemcsak reprodukálták a felfedezett "charmónium" állapotokat, de további rezonanciáik tulajdonságait, valamint a rezonáns szintek közötti elektromágneses átmenetek erősségét is részletesen előrejelezték. Nagyon fontos körülménynek bizonyult, hogy a növekvő tömeggel a kötött állapotok mérete egyre kisebb. Ennek megfelelően az erős "töltés" vagy más szóval erős csatolási állandó értékét a tömeg növekedésével meghatározott módon csökkenőnek választották, amint azt az 1973-ban felfedezett aszimptotikus szabadság tulajdonsága megköveteli. Ezzel a Zweig-szabály "szuper Zweigszabállyá" alakult, hiszen nehéz kvarkokból álló hadronok esetében nemcsak a gluonok minimálisan szükséges száma (a perturbációszámítás rendje), hanem a gluonok csatolásának gyengülése is csökkenti a bomlás valószínűségét.
A spektrumszámolások robbanásszerűen kifejlődő aktivitásába kapcsolódott be Kunszt Zoltán, aki külföldi szerzőtársaival a bájoskvark-spektroszkópia nagyhatású cikkeinek sorát írta meg 1975-77 között [1, 2]. Legnagyobb hivatkozottságú közleményükben [2] - amelynek idézettsége kétszáz fölött van - a könnyű és nehéz mezonok teljes spektroszkópiájának, valamint annihilációs, azaz elektron-pozitron párba történő szétsugárzási szélességeiknek kiszámítására vállalkoztak egyetlen egységes parametrizációjú konsztituens kvarkmodell keretei között. A nemrelativisztikus kvarkmodell használata kritizálható a könnyű mezonok esetében, ám a szerzők célja éppen az volt, hogy ezen számításoknak a nehéz összetevős mezonokkal való szembesítését érvként használhassák a modell utóbbiakra való alkalmazhatósága mellett.
A Harvard és az MIT fizikusai által az első publikációkban használt kvarkok közötti potenciál sikeres vonásait - azaz a kvarkokat bezáró potenciál függetlenségét a kvarkok fajtájától (ízétől) és spinjétől, valamint a Coulomb-jellegű rövidtávú erős potenciált - Kunszt és munkatársai a jellemző paraméterértékekkel együtt átvették. Ezt kiegészítették a konsztituens (anti)kvarkok tömegének összegével és relatív mozgásuk kinetikus energiájával, továbbá a kölcsönhatás spinfüggését a Dirac-egyenletből származtatott, az atomfizikából jól ismert Breit-Fermi-potenciállal. A kinetikus részben a nem-relativisztikus mozgási energia mellett figyelembe vették annak első relativisztikus (úgynevezett Darwin) korrekcióját. Az atomfizikai minta követését jól illusztrálja, hogy spinfüggő potenciál levezetését illetően cikkük lábjegyzete "a relativisztikus kvantummechanika bármelyik standard tankönyvéhez" utalja az olvasót:
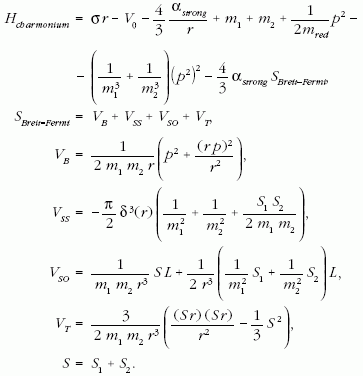
A spinfüggő és relativisztikus korrekciók elhagyásával nyert Schrödinger-hullámfüggvényt megszorozták a spinállapot vektorával, és ezzel a hullámfüggvénnyel a perturbációszámítás első rendjében számolták ki a spinfüggő és a relativisztikus energiajárulékot.
A relativisztikus kinetikus korrekciók nagysága a nehézkvarkos kötött állapotok esetében a nem-relativisztikus mozgási energia tizedének adódott. A könnyű összetevőket is tartalmazó állapotokban hányadosuk egységnyi (vagy még nagyobb) volt, ami mutatta a perturbációszámítás alkalmatlanságát ez utóbbiakra. A cikkben közölt táblázatból azokat a tömegértékeket és (a fotonhoz csatolódó rezonanciákra számolható) leptonikus szélességeket idézi fel az 1. táblázat, amelyekre a nem-relativisztikus számolás a fenti teszt alapján önkonzisztensnek bizonyult. A cikk megjelenésekor mindössze a virtuális fotonhoz csatolódó három Ψ-állapot volt ismert. Látható, hogy a szisztematikusnak mondható eltérések, továbbá a magasabb rezonanciák közül kettőnek nem egyértelmű hozzárendelése ellenére a leírás a mai tömegadatok egyikére sem pontatlanabb 5%-nál. A paramétereknek az elmúlt 35 évben elvégzett mérésekhez történő hangolásával talán még javítani is lehetne az egyezésen.
A charmónium-rendszert 1977-ben az üpsziloncsalád felfedezése követte a 9,5 és 10 GeV/c2 közötti tömegtartományban. Érdekesség, hogy felfedezésének tényét 1977. július 8-án Budapesten, az Európai Fizikai Társaság Nagyenergiás Fizikai Konferenciáján jelentette be Leon Lederman (2. ábra).
Így a konsztituens kvarkok kutatói kevesebb, mint fél évtized alatt két "hidrogénatomot" is kaptak, amelyek szintrendszerével és bomlási erősségeivel a részecskefizikusok sokszorosan ellenőrizhették a kötött kvarkállapotokra vonatkozó elképzeléseiket. A konsztituens kvarkok fogalmának e fejlemények révén mindennapivá lett használata mondatta Zweiggel 2010 februárjában: "constituent quarks are really aces in disguise" azaz "a konsztituens kvarkok valóban álruhás ászok" (Zweig eredetileg az ász nevet javasolta, de Gell-Mann ellenében semmi esélye nem volt a névadásra).
A nagyenergiás hadronütközésekben történő részecskekeltés tulajdonságainak vizsgálatára a partonmodell sokáig nem volt hatással. Ennek oka az, hogy a végállapot kialakulásában a kis impulzusátadású "puha" folyamatok dominálnak. A növekvő energiájú kísérletek végállapotainak növekvő népszerűségű modellje volt az 1970-es évek elején a Rolf Hagedorn által 1965-ben javasolt tűzgolyó-modell, amely két független (az analitikus eredményekben faktorizálódó) lépéssel modellezte a nagyenergiás ütközések végállapotát. Az első (nem-termikus) lépés vezet a nagyon nagy energiasűrűségű, úgynevezett tűzgolyó közbenső állapot létrejöttéhez. A tűzgolyó-állapotot Hagedorn termodinamikailag jellemezte és elbomlását véletlen Markov-folyamatként írta le. Ez azt is jelentette, hogy a végállapoti hadronok keltésében a tűzgolyót létrehozó folyamatnak nincs szerepe: a tűzgolyó hasonló tulajdonságú lehet akár elektron-pozitron annihilációból, akár nehézionok ütközéséből alakul ki.
1972-ben Gálfi és Hasenfratz Péter a mélyen rugalmatlan elektron-proton eloszlásban a virtuális foton elnyelése után kialakuló közbenső állapotból keletkező sok részecske közül egyetlenegynek (legyen a neve A) impulzuseloszlását igyekeztek kinyerni [3]. A Regge-analízis keretei között olyan faktorizált alakot találtak A úgynevezett inkluzív keltési hatáskeresztmetszetére, amelyben az e + p → e? + X folyamat (már bemutatott) hatáskeresztmetszetét egy teljesen hadronikus B + p→A + X folyamat hatáskeresztmetszetéből alkotott kifejezés szorozza. Ez a konklúzió alátámasztotta a kétlépéses mechanizmust, azonban még nem mondott részleteket a folyamat téridőbeli lezajlásáról.
Montvay István 1973-ban a CERN-ben töltött egyéves tanulmányútja során általános megoldását adta a tűzgolyóbomlás úgynevezett statisztikus bootstrap-egyenletének [4]. Ez az integrálegyenlet a tűzgolyó(r) → π(k) + tűzgolyó(r-k) láncfolyamat egymást követő pionsugárzási lépéseit addig folytatja, amíg a visszamaradó tűzgolyó invariáns tömegnégyzete le nem csökken a proton tömegére (a zárójelben lévő kifejezések az egyes objektumok négyes impulzusait jelölik). A keresett mennyiség az r impulzusú tűzgolyó bomlása során kisugárzott nagyszámú részecske adataiból képezhető Lorentz-invariáns egyrészecske-eloszlás:
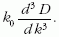
Ezt meghatározza a fenti egyetlen sugárzási lépésben történő kisugárzás valószínűségi sűrűségfüggvénye:
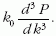
Utóbbit adott tömegű tűzgolyóra a termodinamikai egyensúly feltételezésével egyszerűen lehet parametrizálni. Az integrálegyenlet a kívánt impulzusú pion kisugárzását két eseménykategória összesítésével adja meg. Az alábbi egyenlet jobb oldalán az első tag egyetlen éppen alkalmas pion kisugárzásának járulékát adja, amihez a második tag egy k? impulzusú pion kisugárzása után visszamaradó tűzgolyóból származó pioneloszlás járulékát adja hozzá:
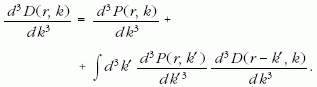
A többváltozós eloszlás statisztikus momentumait, például a részecskeszámot adó nulladik momentumot meghatározó egyenlet jóval egyszerűbb:
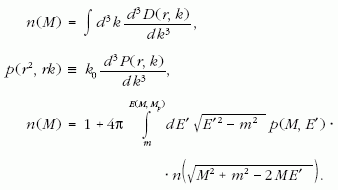
Itt E', az elsőként kisugárzott pion energiája szerint történik az integrálás. Alsó határa a pion tömege, felső korlátja pedig abból a követelményből adódik, hogy a sugárzás után visszamaradó tűzgolyó tömege a protontömegnél nagyobb. Szerencsére a korabeli kísérletekből elsődleges információként éppen a keltett különböző hadronok (elsősorban pionok) multiplicitásai álltak rendelkezésre.
Montvay hazatérése után a megoldás fenomenológiai alkalmazásainak kidolgozására csoportot szervezett Csikor Ferenc, Farkas István és Katona Zoltán részvételével [5], amelyhez később alkalmilag Niedermayer Ferenc is csatlakozott. A kisugárzási események közé az egyetlen π részecske helyére a különböző tömegű, SU(3) íztulajdonságú és spinű reális mezon- és barionspektrum került, ami sokváltozós, csatolt egyenletrendszerek megoldását igényelte. A kvarkok létezése a tűzgolyó kvark-alkotórészeinek feltételezésével és az integrálegyenletek kisugárzási erősséget képviselő tényezőjében a Zweig-szabályt kifejező módosítással jelent meg a statisztikus modellben. A csoport számos reakcióra (például proton-proton, proton-antiproton szórásra) alkalmazta a kvark-tűzgolyó modellt [6]. Az eljárást itt a kutatások kiindulópontját jelentő publikáció legegyszerűbb modellrendszerével illusztrálom [7]. Ez a változat impulzustól függetlenül kizárólag a részecskeszám eloszlásának kérdését kívánta tárgyalni.
A semleges és töltött pionok kisugárzását megengedő modellben a tűzgolyó vagy u vagy d kvark izospin kvantumszámával rendelkezik. A 3. ábra két sugárzási esemény rajzát mutatja. Ha a tűzgolyó aktuálisan sugárzó komponense eredetileg u kvarkból áll, akkor π0 úgy keletkezhet, hogy u-anti-u párkeltés után az eredeti u a pár anti-u tagjával társul és továbbra is u repül tovább. π+ az u-t a d-anti-d pár antikvarkjával kombinálva alakulhat ki és ekkor d repül tovább. A két mezon izospin-hullámfüggvényét ismerve világos, hogy az első eset valószínűsége fele az utóbbiénak. Jelölje Zu az u kvarkból kisugárzott mezonok multiplicitás-eloszlásának generátorfüggvényét és legyen a kisugárzási esemény erősségét jellemző csatolás értéke α. Ekkor a Markov-folyamatok alapfogalmait használva a következő egyenlet írható fel:
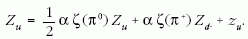
Ebben az egyenletben ξ(πi) a generátorfüggvény megfelelő pionhoz tartozó változója, zu pedig a generátorfüggvény azon határértéke, amelyhez a sugárzási folyamatok lezárultával konvergál. Hasonló megfontolással adódik a d kvark állapotú tűzgolyó sugárzásainak generátorfüggvényére a
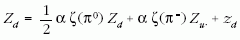
egyenlet. Feltéve, hogy zd = zu, a két egyenlet meg- oldható. A Zu (ξ(π0), ξ(π+), ξ(π-)) generátorfüggvényt változói szerint hatványsorba fejtve polinomiális eloszlást kapunk a különböző pionok adott energiájú ütközésben keletkező sokaságának multiplicitás-eloszlására. Ez az eloszlás - a szabad paraméterek ütközési energiafüggő értékeit alkalmasan választva - a kísérleti eredmények jó leírását adja.
Sokváltozós, csatolt rendszert is konstruáltak arra az esetre, amikor a teljes pszeudoskalár oktettet és hozzá a vektormezon oktettet is önálló eloszlásfüggvénnyel jellemezték. A Gell-Mann-i óvatos felfogást tükrözi cikkük záró bekezdése, ahol a következőket írják: "itt a kvarkok nem feltétlenül fizikai objektumok abban az értelemben, hogy a modell azonos alakban fogalmazható meg azon alapállásból is, hogy a tűzgolyóállapotok (meghatározott ágarányú bomlásállandóikkal) a matematikai kvarkállapotok direktszorzatával azonosan transzformálódnak".
Ebből a kutatói óvatosságból Niedermayer Feri ugyanebben az évben továbblépett, teljes mértékben csatlakozva Feynmannak a nagy impulzussal meglökött kvarkok evolúciójára Balatonfüreden bemutatott elképzeléseihez. Nagy visszhangot kiváltó cikke (70 körüli független hivatkozás) a hirtelen impulzusátadással a nukleonból kilökött kvark hadronsugárzását nemcsak a kvantumszámok evolúciója szempontjából tárgyalja, hanem az impulzusveszteség leírását is megadja [8]. Faktorizált alakot tételez fel annak valószínűségi jellemzésére, hogy egyetlen sugárzási aktusban egy α típusú, p impulzusú kvark i fajta, zp impulzusú piont sugározzon ki (z < 1):
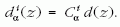
Az izospinfaktor és az impulzuseloszlás sugárzási aktusok sorozatában bekövetkező alakulására önálló összefüggés írható fel. Például egy u kvarkból z impulzushányadú π0 pion létrejöttének valószínűségét megadó úgynevezett fragmentációs függvényt D(z)/3 alakban érdemes parametrizálni. Niedermayer D(z )-re a fent tárgyalt tűzgolyóegyenlet származtatásával azonos megfontolás alapján inhomogén integrálegyenletet származtatott, ahol az inhomogén tag nyilván d(z):
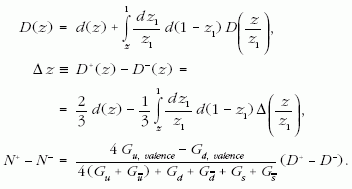
A második-harmadik sor a pozitív és negatív töltésű pionok aszimmetriájának (az izospineloszlás fejlődésének) egyenletét adja, amellyel a 4. sor egyenletét használva lehet jóslatot tenni a kétféle részecske számában várható detektálási aszimmetriára. Az integrálegyenlet megoldása figyelmet igényel, mivel z = 0 körül az egyenlet és vele D(z) is szinguláris. A szingularitás viszont kiesik a töltött pionok longitudinális eloszlásának aszimmetriáját leíró kombinációból (2-3. sor). A kapott megoldás lehetővé teszi a multiplicitások z-függésének tanulmányozását. Ez az elmélet megadja a skálainvariáns kollineáris közelítést a kvarksugarak (jetek) kifejlődésére, amihez a QCD a skálainvarianciát logaritmikusan sértő járulékokat generál. A nagyenergiás (kemény) jetek fizikája a QCD talán legsikeresebb fenomenológiai alkalmazása, ám a szemléletet formáló értelmezést a partonmodell adta meg!
A "novemberi forradalom" után a kvarkok létezése általánosan elfogadott ténnyé vált. Az aszimptotikus szabadság tulajdonságának felfedezésével 1973-ban a QCD bizonyította, hogy megoldásában a nagyenergiás és nagy impulzusátadással járó kinematikai tartományban alkalmazható a perturbációszámítás. A Puskin utcában az évtized közepén mégsem kezdtünk a kvantumkromodinamika perturbatív vizsgálatához. Ennek fő oka az volt, hogy mindnyájan (és világszerte sok más elméleti fizikus is) úgy éreztük, hogy a QCD alapkérdése a Lagrange-sűrűségében szereplő kvantumterek, a kvarkok és gluonok kvantumjainak megfigyelhetetlensége. Ezt a perturbatív megoldás egyáltalán nem kezeli. A kvarkbezárás jelensége döntő kérdés mind a könnyű kvarkok kötött állapotainak spektroszkópiája, mind a nagyenergiás folyamatokban keletkező részecskék zömét alkotó úgynevezett puha (kis négyes-impulzusú) mezonok tulajdonságainak megértése szempontjából.
A részecskefizika e két "történelmi" jelenségkörét jellemző méretskálán a QCD csatolási állandója megnő és kilép a perturbációszámítás tartományából. Az igényelt nem-perturbatív megoldás módjára számos (máig élő és máig sem bizonyított) javaslat született az 1970-es évek közepén (1/Nc kifejtés, instantonkonfigurációk vagy monopólus-konfigurációk dominanciája, rácstérelméleti tárgyalás és mások), de a kvarkbezárás kielégítő térelméleti tárgyalására (például a kvark-antikvark forrás között ható kölcsönhatási potenciál nagy távolságon érvényes alakjának kiszámítására) azidőtájt egyik sem volt képes. Az alkalmazásokban érdekelt gyakorlatias megközelítés (időlegesen) "lemondott" a kvarkbezárás térelméleti bizonyításáról. Szemléletes kiegészítő fenomenológiai előírással - nagy méretskálán - "letiltották" a kvantumkromodinamika alkotórészeinek észlelhető megjelenését: 1974 elején Chodos, Jaffe, Johnson, Thorn és Weisskopf publikálták az erősen kölcsönható részecskék úgynevezett MIT-zsák modelljét.
A hadron belsejét a kvarkmentes külvilágtól a zsákállandónak nevezett pozitív térfogati energiasűrűség különbözteti meg. A kvarkok lokális hatása "emeli ki" környezetükben a vákuumot nem-perturbatív alapállapotából a magasabb energiasűrűségű állapotba. A zsákot az tartja felfújva, hogy a zsákállandóból származó negatív nyomást a kvarkokból és gluonterükből származó pozitív nyomás egyensúlyozza. A zsák felületén a gluontér "színes elektromos" komponensei a felülettel párhuzamosak, "mágneses" komponensei arra merőlegesek, így a hadronnak a külvilágba mutatott színfluxusa (-töltése) nulla (nem-ábeli Gauss-tétel) és a külvilággal nem cserél gluonkvantumot sem (a nemábeli Poynting-vektor normális komponense nulla). A zsák belsejében a kvarkterek a Dirac-egyenletet oldják meg a zsák falánál előírt, a kvarkok kijutását letiltó határfeltételekkel. A Dirac-egyenletben figyelembe veszik a kvarkok keltette belső gluonteret is.
A határ az elektromágneses tér és az a leptonok számára átjárható, így a kvarkok nagy impulzusátadással járó elektrogyenge kölcsönhatása az elektronokkal, müonokkal vagy neutrínókkal a kísérletekkel összhangban írható le. A meglökött kvarkok hatására a zsák csőszerűen deformálódik és a kialakuló színfluxuscső energiája a cső hosszával arányosan nő. Ez a folyamat szemléletesen leírja a nagy gerjesztettségű hadronok esetében kialakuló húrgeometriát, amelyre Nambu és Veneziano az 1960-as évek második felében az S-mátrix elméleti Regge-aszimptotikából indulva jutott el. A sokrészecskés végállapot a húr darabolódásával "születik meg". A fluxuscső erős színelektromos terében kipolarizálódó kvark-antikvark párt a rajtuk végződő fluxusok zárják különálló zsákokba (4. ábra).
Az MIT-zsák geometriai felülete nem rendelkezik önálló dinamikával, a leírt folyamat tárgyalásának adekvát módja a molekulafizika Born-Oppenheimer-közelítésének adaptálása: a zsák alakját a kimozdított pontszerű kvark és a visszamaradó dikvark között kialakuló gluontér körül tengelyszimmetrikusan parametrizálják, az egyensúly feltételével méretét meghatározzák, majd adiabatikus közelítést alkalmazva, az alakkal "pillanatszerűen" követik a gyorsan távolodó kvarkot.
 |
 |
Kuti Gyula második MIT-ban töltött vendégkutatói évéről 1974 őszén tért vissza az ELTE-re. Nem szerepelt a zsákmodell szerzői listáján, mert ezt az évet a kvantumtérelmélet nem-perturbatív megoldási módszerének keresésére szánta, idejét az atomfizikából Rayleigh-Ritz-módszerként ismert eljárás kvantumtérelméleti változatának kidolgozásával töltötte. Ennek igen furcsa formában maradt nyoma a szakirodalomban. A "2PI-közelítés" néven ismert eljárásról szóló talán legnagyobb (1000 fölötti) idézettségű cikknek, Cornwall, Jackiw és Tomboulis munkájának V.C alfejezetében a szerzők, J. Kutinak köszönetet mondva, közlik a módszer Kuti által, tőlük függetlenül megalkotott tárgyalását (lásd 5. ábra).
A ma is nagyon önkritikusan dolgozó és ritkán publikáló Kuti számításai végén valószínűleg meggyőzte magát arról, hogy ez a közelítés sem visz igazán közel a kvarkbezárás térelméleti tárgyalásához. Így "elajándékozta" eredményeit, és csatlakozott a zsákmodellek fejlesztésének ígéretesebbnek látszó irányzatához.
Itthon az Atomfizikai Tanszéken kezdte szervezni azt az új csapatot, amellyel a zsákmodell számára kielégítőbb változatának vizsgálatához fogott. A régiek közül csak Gnädig maradt, a téma kedvéért társult Hasenfratz Péter, Kunszt Zoltán és Szalay Sándor. Kuti szuggesztív személyiségének hatását jól mutatja, hogy mindhármójuknak volt ezt megelőzően vagy akár párhuzamosan más sikeres kutatási témája, mégis szövetkeztek vele a később Budapest-zsák nevet kapott új modell kidolgozására.
Kuti eredetileg két stratégia mentén tartotta elképzelhetőnek az MIT-zsák tökéletesítését. Az úgynevezett "puha zsák" elképzelés a fluxuscső kialakulását a QCD téregyenletek falmentes megoldásától reméli. Ennek mintáját az elektrodinamika egy olyan modellje adta, amelyben az elektromágneses tér forrásait tökéletesen diaelektromos (az elektromos fluxust kitaszító) közeg veszi körül. E közeg térelméleti leírására t'Hooft egy skalár "dielektromos" tér bevezetését javasolta 1974-ben. A skalár tér nem-nulla értéke (kondenzálódása) alakítja ki az elektromos teret a közegből kiszorító hatást, amely lokalizálja a fluxust a forrás és a nyelő töltések közötti csőszerű tartományra.
Számos szerző felfigyelt arra, hogy a szupravezetés Ginzburg-Landau-modelljéből Abrikoszov által levezetett mágneses fluxuscső-megoldás fluxusának forrásául és nyelőjéül éppen alkalmas egy Dirac-féle mágneses monopólus-antimonopólus pár. Ezzel egy véges hosszúságú mágneses fluxuscső alakul ki, amelynek energiája a cső hosszával arányos. Ha elektromágneses világunk alapállapota szupravezető lenne, a fenti megfigyelés magyarázná a magányos mágneses monopólusok megfigyelésének hiányát. Nielsen és Olesen 1973-ban relativisztikus térelméletbe ágyazta a Ginzburg-Landau-elméletet. Az elektrodinamika jól ismert E ↔ -B dualitási invarianciája alapján az elektromosan töltött Cooper-pár kondenzátum helyett mágnesesen töltött monopólus-kondenzátumot feltételezve adódik egy elektromos fluxuscső-megoldás, amely állandó erővel hat az elektromos töltésre, azaz aszimptotikus eltávolodását végtelen energia befektetésével teszi csak lehetővé.
Nambu és Mandelstam nyomán 1975-ös cikkében Giorgio Parisi fogalmazta meg először azt a feltevést, hogy a QCD alapállapotában véges mágneses töltéssűrűség kondenzálódik, és ez magyarázza a kromoelektromos fluxussal rendelkező (színes) állapotok megfigyelhetetlenségét (ezt az elképzelést mindmáig aktívan igyekeznek bizonyítani rácstérelméleti szimulációkkal). Az ő munkájának előnyomatát adta kezembe Kuti az Elméleti Fizika Tanszék folyosóján azzal, hogy a röviden vázolt ideát próbáljam részletesebben kidolgozni. Ebből az indíttatásból született három cikkemben [9] először az ábeli U(1) szimmetrikus elmélet klasszikus duális megoldását meghatározó egyenleteket vizsgáltam, majd kollektív koordinátákat keresve a rendszer húrszerű rezgéseinek kvantálására tettem kísérletet, végül a megoldások nem-ábeli elméletbeli beágyazását követően érveket kerestem arra, hogy a fluxuscső-megoldások legalacsonyabb energiájú konfigurációi a csoport centrumához tartozó, tehát alapvetően ábeli térkonfigurációk lesznek. Szerencsés egybeesés volt, hogy Frenkel Andor, Hraskó Péter, Horváth Zalán és Palla László érdeklődése ez idő tájt, más-más okból, szintén a mágneses monopólusok felé fordult.
Kuti és új csoportja Budapest-zsák modelljének definíciója során megmaradt az MIT kutatói által bevezetett éles határfelület mellett. A klasszikus zsákmegoldáson túllépő célt tűztek ki: kvantumos tárgyalást kívántak adni az alapállapoti konfiguráció összes kis rezgésére. Ebből a szempontból szerencsésebbnek tűnt olyan modellt választani, amelyben a felületi pontok önálló dinamikájú szabadsági fokként jelennek meg. Ezzel indokolták, hogy a határfelületre a membránokat jellemző felületi feszültséget vezettek be. Az alábbi hatás ehhez kapcsolódó járuléka mozgásegyenletet eredményezett a felület pontjaira is:
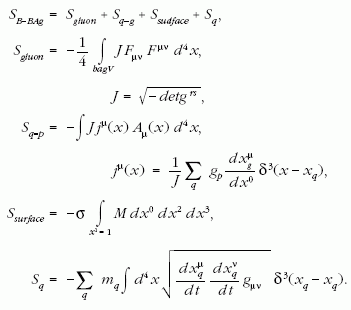
Végül egyetlenegy cikket jelentettek meg referált folyóiratban [10], amely jelzésszerűen foglalta össze igen részletes vizsgálataik eredményeit. Egyidejűleg számos előadást tartottak műhelyeken és nemzetközi konferenciákon, de eredményeik rendszeres publikálását nem érezték még időszerűnek.
A négyszerzős közlemény az ábeli rendszer klasszikus mechanikai Hamilton-egyenleteit elemezte általános görbevonalú koordinátarendszerben. Diracnak az úgynevezett szinguláris mechanikai rendszerekre kidolgozott elméletével kezelték az önálló dinamikával nem rendelkező, kényszer-jellegű általánosított koordinátákat, amellyel előkészítették a valóban független dinamikai szabadsági fokok kanonikus kvantálását. A tengelyszimmetrikus esetre meghatározták a töltött forrás és nyelő között kialakuló térkonfigurációt és sikeresen illesztették a sztatikus konfiguráció energiáját egy Coulomb-szerű és egy lineárisan növekvő tagból álló potenciál összegéhez (6. ábra). Vizsgálták a gluontér kis rezgéseiből, továbbá a membrán rezgéseiből létrejövő gerjesztések spektrumát.
Érdekes "mellékterméke" volt a modell vizsgálatának az a "historikus lelet", hogy Dirac a müon senki által nem várt felfedezése kapcsán egy tisztán felületi feszültséggel rendelkező kiterjedt lepton "zsák" gömbszimmetrikus kvantum-konfigurációiként igyekezett az elektront és attól csak tömegében eltérő nehéz "testvérét" értelmezni. Gnädig és Kunszt részletesen vizsgálta a Dirac-elektront és rámutatott a gömbi szimmetriától eltérő deformációkkal szembeni instabilitására [11]. A Dirac-elektron általuk adott letisztult tárgyalását követő újabb cikkek a modellt gravitációs hatással kiegészítve érvelnek a rendszer stabilizálhatósága mellett.
1977-ben Hasenfratz és Kuti megírta azt a zsákmodellekről szóló összefoglaló tanulmányt [12], amelyet Pickering "történelemkönyve" is első helyen ajánl a hadronzsákok elméletének technikai vonatkozásai iránt érdeklődőknek. Bár a nagy összefoglaló cikk a zsák-típusú modelleket alkalmazó részecske- és magfizikusok bibliája lett (300 hivatkozás), a felületi feszültség kvantumszintű kezelése túl bonyolult technikai kihívásnak bizonyult, az MIT-zsákkal nyerhető eredményektől eltérő jóslatok ellenőrizhetősége pedig kérdéses maradt. A geometriailag értelmezett kiterjedt részecskemodell kutatásának folytatása egyre kockázatosabbá vált a kvantumtérelmélet más megoldási technikái fejlődési iramának és az oda összpontosuló kutatói erőfeszítésnek gyorsuló növekedése láttán.
Az 1980-as évtizedben Gálfi és Gnädig érdeklődése egyre inkább a klasszikus fizika klasszikus szépségű feladatai, valamint a középiskolai tehetségek nevelése felé fordult. Már a hetvenes években beindult a perturbatív QCD nagyenergiás jet-fizikai alkalmazásainak a kísérleti megfigyelésekhez szorosan kapcsolódó fejlesztése. Kunszt Zoltán az évtized vége felé (kis kitérőkkel) végleg ehhez a irányzathoz csatlakozott és sikereit a zürichi ETH professzori meghívással ismerte el. A többiek viszont az 1980-as évek elejére, egymástól lényegében függetlenül ugyanabba, a színbezárás problémájának megoldását ígérő irányba fordultak. Legalább egy évtizedre a kvantumkromodinamika téridőrácsos megoldásának irányzatához csatlakoztunk.
Hasenfratz Péter Hasenfratz Anna diplomamunkással közös munkájában egy alapvető fontosságú mennyiség kiszámításával tette le névjegyét: a QCD rácstérelméleti számolásokban használt dimenziós paraméterét összekapcsolták a jet-fizikai számolásokban használt karakterisztikus impulzusskálával. Hasenfratz végül a nyolcvanas évek közepétől a Berni Egyetem professzoraként talált rá állandó szerzőtársára, Niedermayer Ferencre. Kuti Gyula Szlachányi Kornéllal és Polónyi Jánossal együttműködésben a világon elsőként számítógépes rácstérelméleti módszerrel vizsgálta a hadronfázis - véges hőmérsékletű fluktuációk hatására bekövetkező - átalakulását kvarkfázisba. Pályáján mindmáig törekszik az alapkérdések eredeti megközelítésű vizsgálatára. Rossz véleménye van a nehéznek bizonyult problémákat az "út szélén hagyó", a gyorsan learatható kérdésekre vadászó kutatói stílusról. Nem lephetett hát meg senkit, amikor a University of California (San Diego) professzora 2005-ben újra nekifutott a hadrongerjesztések húrszerű viselkedésére vezető mechanizmus ab initio számítással való feltárásának. Montvay István korábbi bielefeldi munkatársaival együttműködve szintén a QCD termodinamikájának vizsgálatával indította pályája új szakaszát, amelyet a Hamburgi Egyetem nagy számítógépes térelméleti kooperációkat szervező professzoraként, egyben a legelterjedtebben használt rácstérelméleti monográfia társszerzőjeként teljesített ki. Jómagam Ruján Pál és Deák Ferenc kollégáimmal a véges rácsállandójú mértékelméleti rendszerekre alkalmazott statisztikus fizikai variációs módszerekkel keltettem nemzetközi figyelmet.
A kvarkfizika történetének második évtizedében végzett munka kutatói stílusunkra mindmáig rányomja bélyegét. Egyikünk sem érdeklődött tartósan a modellépítés, az új szimmetriákat, új szabadsági fokokat feltételező elméleti modellek konstrukciója iránt. Mindannyian a Standard Modell (esetleg annak minimális tágítását jelentő modellek) kvantumdinamikájának minél nagyobb elméleti tisztaságú megoldására tettünk és teszünk erőfeszítéseket. Ez a kutatói érdeklődés és stílus átsugárzott a QCD kutatásában bennünket követő generációra is. Fodor Zoltánt, Trócsányi Zoltánt, Petreczky Pétert világszerte a finom megközelítést igénylő dinamikai kérdések kiemelkedő aktivitású magyar szakembereiként tartják számon.
És végül: a kvarkok dinamikájának Puskin utcai kutatását kezdeményező barátunk, Kuti Gyula 1940. november elsején született. Éljen és dolgozzon soká!