Fizikai Szemle honlap |
Tartalomjegyzék |
 |
 |
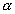 beesési szöggel érkező fénysugár
iránya megtörik, ha egy másik közeg (pl. víz) határához
érkezik. Az
beesési szöggel érkező fénysugár
iránya megtörik, ha egy másik közeg (pl. víz) határához
érkezik. Az 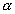 beesési szög és a megtört sugár
beesési szög és a megtört sugár
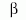 törési
szögére a következő egyenlet teljesül: sin
törési
szögére a következő egyenlet teljesül: sin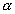 / sin
/ sin
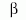 = n,
ahol n az anyag törésmutatója, ami a fény levegőben és
közegben mért terjedési sebességének az arányával egyezik
meg. A Nap fénye közel párhuzamosan érkezik az
esőfelhőben lévő vízcseppek felületéhez. Egy fénysugár
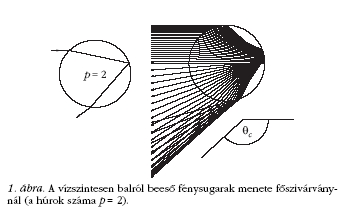
menete egyszeres belső visszaverődés esetén az 1. ábra
bal oldali részén látható (a belső visszaverődések száma
helyett az irodalomban szokásos módon, a vízcseppen
belüli húrok p számát adtuk meg). Descartes nagy türelemmel,
körzővel és vonalzóval, illetve a Snellius-Descartes-
törvényt felhasználva szerkesztette meg közel száz
párhuzamosan beeső fénysugár menetét. Ma már könnyen
írhatunk olyan számítógépes programot, amellyel
ezt a feladatot gyorsan megoldhatjuk. Az eredmény a 1.
ábra jobb oldali részén látható. A vízcseppből kilépő
fénysugarak irányát jellemezhetjük a
= n,
ahol n az anyag törésmutatója, ami a fény levegőben és
közegben mért terjedési sebességének az arányával egyezik
meg. A Nap fénye közel párhuzamosan érkezik az
esőfelhőben lévő vízcseppek felületéhez. Egy fénysugár
menete egyszeres belső visszaverődés esetén az 1. ábra
bal oldali részén látható (a belső visszaverődések száma
helyett az irodalomban szokásos módon, a vízcseppen
belüli húrok p számát adtuk meg). Descartes nagy türelemmel,
körzővel és vonalzóval, illetve a Snellius-Descartes-
törvényt felhasználva szerkesztette meg közel száz
párhuzamosan beeső fénysugár menetét. Ma már könnyen
írhatunk olyan számítógépes programot, amellyel
ezt a feladatot gyorsan megoldhatjuk. Az eredmény a 1.
ábra jobb oldali részén látható. A vízcseppből kilépő
fénysugarak irányát jellemezhetjük a 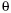 szórási szöggel,
ami a belépő és kilépő sugár közti szög. Az 1. ábrából
szembetűnő, hogy a vízcseppből kilépő összes fénysugár
szórási szöggel,
ami a belépő és kilépő sugár közti szög. Az 1. ábrából
szembetűnő, hogy a vízcseppből kilépő összes fénysugár
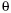 szórási szöge nagyobb egy
kritikus
szórási szöge nagyobb egy
kritikus 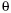 c szögnél.
A
c szögnél.
A 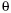 c
szög csak a víz n törésmutatójától és a húrok p számától
függ [4]. Ezt a speciális sugármenetet Cartesius-sugárnak
nevezzük. Jól látható az 1. ábrából, hogy a Cartesius-sugármenet
közelében beeső párhuzamos sugarak a vízcseppből
kilépve közel párhuzamosak maradnak, a nyaláb
ebben az irányban a legintenzívebb [4]. Más esetekben
a nyaláb a vízcseppből kilépve szétszóródik. Így a
Cartesius-sugármenetnek kitüntetett szerepe van. Pontos
matematikai számításokkal megmutatható, hogy a főszivárványt
a bejövő fénysugár irányához képest
c
szög csak a víz n törésmutatójától és a húrok p számától
függ [4]. Ezt a speciális sugármenetet Cartesius-sugárnak
nevezzük. Jól látható az 1. ábrából, hogy a Cartesius-sugármenet
közelében beeső párhuzamos sugarak a vízcseppből
kilépve közel párhuzamosak maradnak, a nyaláb
ebben az irányban a legintenzívebb [4]. Más esetekben
a nyaláb a vízcseppből kilépve szétszóródik. Így a
Cartesius-sugármenetnek kitüntetett szerepe van. Pontos
matematikai számításokkal megmutatható, hogy a főszivárványt
a bejövő fénysugár irányához képest 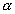 2 =
180°-
2 =
180°-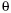 c(p = 2) = 42,5°
irányból látjuk legintenzívebbnek
vörös színű fényre (azaz n =1,330 törésmutatóval számolva)
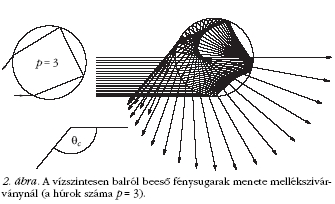
[4]. Hasonló módon alakul ki a halványabb mellékszivárvány,
amikor a vízcseppen belül két visszaverődés
történik (a húrok száma p = 3). Ekkor a balról párhuzamosan
beeső sugarak a 2. ábra szerint egy kritikus
c(p = 2) = 42,5°
irányból látjuk legintenzívebbnek
vörös színű fényre (azaz n =1,330 törésmutatóval számolva)
[4]. Hasonló módon alakul ki a halványabb mellékszivárvány,
amikor a vízcseppen belül két visszaverődés
történik (a húrok száma p = 3). Ekkor a balról párhuzamosan
beeső sugarak a 2. ábra szerint egy kritikus
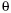 c(p=3) szögnél kisebb
szórási szöggel lépnek ki a vízcseppből
(megjegyezzük, hogy
c(p=3) szögnél kisebb
szórási szöggel lépnek ki a vízcseppből
(megjegyezzük, hogy 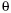 c
(p=3) <
c
(p=3) < 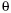 c
(p =2)). A
mellékszivárványt a bejövő fénysugár irányához képest
c
(p =2)). A
mellékszivárványt a bejövő fénysugár irányához képest
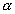 3 = 180° -
3 = 180° -
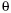 c (p = 3) = 50,1°
irányból látjuk legintenzívebbnek
vörös színű fényre (azaz n =1,330 törésmutatóval
számolva) [4].
A fentiek alapján már könnyen megérthetjük, hogy
miként alakulnak ki a szivárvány ívei. A 3. ábra az esőfelhő
két különböző helyén lévő vízcseppben a Cartesius-
sugármenetet mutatja vörös színre a fő- és a mellékszivárványnál.
Mint láttuk, ezekből az irányokból érkezik
az esőcseppekről a legintenzívebb fény egy távoli P megfigyelőhöz.
Ha a cseppből kilépő Cartesius-sugár egyenesét
a P pont körül úgy forgatjuk el, hogy közben az egyenes
mindig
c (p = 3) = 50,1°
irányból látjuk legintenzívebbnek
vörös színű fényre (azaz n =1,330 törésmutatóval
számolva) [4].
A fentiek alapján már könnyen megérthetjük, hogy
miként alakulnak ki a szivárvány ívei. A 3. ábra az esőfelhő
két különböző helyén lévő vízcseppben a Cartesius-
sugármenetet mutatja vörös színre a fő- és a mellékszivárványnál.
Mint láttuk, ezekből az irányokból érkezik
az esőcseppekről a legintenzívebb fény egy távoli P megfigyelőhöz.
Ha a cseppből kilépő Cartesius-sugár egyenesét
a P pont körül úgy forgatjuk el, hogy közben az egyenes
mindig 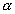 2, illetve
2, illetve
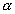 3 szöget zárjon be a bejövő fény
irányával (a 3. ábrán vízszintes vonal), akkor az egyenes
egy kúppaláston mozog, és a cseppekből induló végpontja
egy körívet ír le, amely a szivárvány íve adott
színű fénysugárra. A víz törésmutatója függ a fénysugár
színétől, ezért az
3 szöget zárjon be a bejövő fény
irányával (a 3. ábrán vízszintes vonal), akkor az egyenes
egy kúppaláston mozog, és a cseppekből induló végpontja
egy körívet ír le, amely a szivárvány íve adott
színű fénysugárra. A víz törésmutatója függ a fénysugár
színétől, ezért az 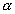 2 és
2 és
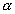 3 szögek nagysága is. Egyszerű
számítások szerint főszivárványnál
3 szögek nagysága is. Egyszerű
számítások szerint főszivárványnál 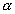 2 vörös színre nagyobb,
mint kék színre, így a külső ív vörös, a belső kék
színű, ahogy ezt a természetben megfigyelhetjük. Mellékszivárványnál
a számítások szerint a színek sorrendje, a
megfigyelésekkel összhangban, fordított a főszivárványhoz
képest [4]. Megmutatható, hogy a 42,5°-os és 50,1°-
os szögek közti irányban (a fő- és mellékszivárvány között)
egy sötét tartomány alakul ki, az Alexander-féle
sötét sáv [4].
A továbbiakban a szivárványnak a fény hullámtermészetén
alapuló elméletét ismertetjük. Közismert a fénynek
a hullámtermészetéből fakadó két alapvető tulajdonsága:
a polarizálhatósága és az interferencia-képessége. A
szivárvány jelenségének jobb megértésében nem tekinthetünk
el a fény e két tulajdonságától. A vízcseppeken
megtörő fény polarizálódik, és így a szivárványról érkező
fény síkban poláros. A fény polarizációjáról bővebben
Härtlein Károlynak a Mindentudás az iskolában sorozat
2006. márciusi számában megjelent cikkét, illetve e cikk
szerzőjének korábbi tanulmányát [4] javasoljuk az érdeklődő
olvasó számára.
Időnként a főszivárvány belső köríve alatt járulékos
íveket is megfigyelhetünk, amelyekre pontos matematikai
elméletet elsőként George Biddell Airy adott 1838-
ban. Röviden tekintsük át az elmélet főbb gondolatát! A
vízcseppre különböző beesési szöggel érkező "fénysugarak"
azonos idő után különböző utat tesznek meg. Ezért
a 4. ábra bal oldalán látható, a bejövő fénysugarakra
merőleges síkú AB hullámfront a vízcseppből kilépve
már nem lesz sík. Kiszámítottuk, hogy a vízcseppen való
áthaladás után miként torzul a hullámfront, az eredményt
a A'C'B' görbe mutatja. Látható, hogy a hullámfront a
C' pontban "megtörik", de minden elemi szakasza továbbra
is merőleges lesz az adott elemi szakaszon átmenő
fénysugárra. A 4. ábra jobb oldali részén a hullámfront
időbeli fejlődése látható. Mivel minden hullámfront
két "megtört" szakaszból áll, ezek különböző hosszúságú
utakat tesznek meg a megfigyelőig, és így egymással interferálnak.
Az ábrán jól látható, hogy a nyíllal jelzett irányokban
erősítik egymást a frontok. Ezekben az irányokban
láthatók a járulékos ívek. Airynek sikerült közelítőleg
kiszámítani a megfigyelőhöz érkező fény intenzitásának a
szögfüggését [4]. Az Airy-elmélet jól közelíti a mért szögfüggést,
és csak kisméretű vízcseppekre (R
2 vörös színre nagyobb,
mint kék színre, így a külső ív vörös, a belső kék
színű, ahogy ezt a természetben megfigyelhetjük. Mellékszivárványnál
a számítások szerint a színek sorrendje, a
megfigyelésekkel összhangban, fordított a főszivárványhoz
képest [4]. Megmutatható, hogy a 42,5°-os és 50,1°-
os szögek közti irányban (a fő- és mellékszivárvány között)
egy sötét tartomány alakul ki, az Alexander-féle
sötét sáv [4].
A továbbiakban a szivárványnak a fény hullámtermészetén
alapuló elméletét ismertetjük. Közismert a fénynek
a hullámtermészetéből fakadó két alapvető tulajdonsága:
a polarizálhatósága és az interferencia-képessége. A
szivárvány jelenségének jobb megértésében nem tekinthetünk
el a fény e két tulajdonságától. A vízcseppeken
megtörő fény polarizálódik, és így a szivárványról érkező
fény síkban poláros. A fény polarizációjáról bővebben
Härtlein Károlynak a Mindentudás az iskolában sorozat
2006. márciusi számában megjelent cikkét, illetve e cikk
szerzőjének korábbi tanulmányát [4] javasoljuk az érdeklődő
olvasó számára.
Időnként a főszivárvány belső köríve alatt járulékos
íveket is megfigyelhetünk, amelyekre pontos matematikai
elméletet elsőként George Biddell Airy adott 1838-
ban. Röviden tekintsük át az elmélet főbb gondolatát! A
vízcseppre különböző beesési szöggel érkező "fénysugarak"
azonos idő után különböző utat tesznek meg. Ezért
a 4. ábra bal oldalán látható, a bejövő fénysugarakra
merőleges síkú AB hullámfront a vízcseppből kilépve
már nem lesz sík. Kiszámítottuk, hogy a vízcseppen való
áthaladás után miként torzul a hullámfront, az eredményt
a A'C'B' görbe mutatja. Látható, hogy a hullámfront a
C' pontban "megtörik", de minden elemi szakasza továbbra
is merőleges lesz az adott elemi szakaszon átmenő
fénysugárra. A 4. ábra jobb oldali részén a hullámfront
időbeli fejlődése látható. Mivel minden hullámfront
két "megtört" szakaszból áll, ezek különböző hosszúságú
utakat tesznek meg a megfigyelőig, és így egymással interferálnak.
Az ábrán jól látható, hogy a nyíllal jelzett irányokban
erősítik egymást a frontok. Ezekben az irányokban
láthatók a járulékos ívek. Airynek sikerült közelítőleg
kiszámítani a megfigyelőhöz érkező fény intenzitásának a
szögfüggését [4]. Az Airy-elmélet jól közelíti a mért szögfüggést,
és csak kisméretű vízcseppekre (R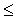 0,1 mm),
illetve
0,1 mm),
illetve 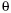 >>
>>
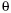 c szögekre (a főszivárvány irányától "távol")
nem ad helyes eredményt.
Meglepő módon csak a 20. század elején sikerült kidolgozni
a szivárvány értelmezésének egzakt elméletét. A
vízcseppre érkező fény elektromágneses síkhullámnak
tekinthető. Ez a síkhullám szóródik a vízcseppen. Az E
elektromos és B mágneses tereket a Maxwell-egyenletek
írják le. Ezen egyenletek alapján tetszőleges méretű és
törésmutatójú gömb alakú anyag fényszórására elsőként
1890-ben Ludvig V. Lorenz, majd jóval később, tőle függetlenül,
1908-ban Gustav Mie, és egy évvel később henger
alakú szórótestekre Peter J.W. Debye vezetett le analitikus
megoldást (az irodalomban az egzakt elméletet egyszerűen
Mie-elméletnek nevezik). Numerikus szempontból
reménytelennek látszott abban az időben az elmélet
jóslatait összevetni a kísérleti eredményekkel. Sokáig
feledésbe is merült az elmélet. Csak az utóbbi évtizedekben,
a számítógépes lehetőségek javulásával került ismét
az érdeklődés középpontjába a Mie-elmélet [4]. Segítségével
sikerült értelmezni két másik, közismert légköroptikai
jelenséget, a koszorút és a glóriát is [4]. Végül érdemes
megjegyezni, hogy a 20. századbeli fizika egyik legfontosabb
eredménye, a kvantummechanika alapján több
neves fizikus is rámutatott a szivárvány és az atomokon
szóródó részecskék kvantummechanikai szórási problémája
közti hasonlóságra [4].
Arisztotelész óta több neves fizikus tanulmányozta az
egyik legismertebb és legszebb légköri jelenséget, a szivárványt.
A szivárvánnyal kapcsolatos jelenségek egzakt
tárgyalása nem nélkülözheti mindazt a tudást, amit a
fényről tudunk. Az optika tudományának fejlődésében
mindig nagy szerepet játszott az újabb elméletek alkalmazása
a szivárvány leírására.
c szögekre (a főszivárvány irányától "távol")
nem ad helyes eredményt.
Meglepő módon csak a 20. század elején sikerült kidolgozni
a szivárvány értelmezésének egzakt elméletét. A
vízcseppre érkező fény elektromágneses síkhullámnak
tekinthető. Ez a síkhullám szóródik a vízcseppen. Az E
elektromos és B mágneses tereket a Maxwell-egyenletek
írják le. Ezen egyenletek alapján tetszőleges méretű és
törésmutatójú gömb alakú anyag fényszórására elsőként
1890-ben Ludvig V. Lorenz, majd jóval később, tőle függetlenül,
1908-ban Gustav Mie, és egy évvel később henger
alakú szórótestekre Peter J.W. Debye vezetett le analitikus
megoldást (az irodalomban az egzakt elméletet egyszerűen
Mie-elméletnek nevezik). Numerikus szempontból
reménytelennek látszott abban az időben az elmélet
jóslatait összevetni a kísérleti eredményekkel. Sokáig
feledésbe is merült az elmélet. Csak az utóbbi évtizedekben,
a számítógépes lehetőségek javulásával került ismét
az érdeklődés középpontjába a Mie-elmélet [4]. Segítségével
sikerült értelmezni két másik, közismert légköroptikai
jelenséget, a koszorút és a glóriát is [4]. Végül érdemes
megjegyezni, hogy a 20. századbeli fizika egyik legfontosabb
eredménye, a kvantummechanika alapján több
neves fizikus is rámutatott a szivárvány és az atomokon
szóródó részecskék kvantummechanikai szórási problémája
közti hasonlóságra [4].
Arisztotelész óta több neves fizikus tanulmányozta az
egyik legismertebb és legszebb légköri jelenséget, a szivárványt.
A szivárvánnyal kapcsolatos jelenségek egzakt
tárgyalása nem nélkülözheti mindazt a tudást, amit a
fényről tudunk. Az optika tudományának fejlődésében
mindig nagy szerepet játszott az újabb elméletek alkalmazása
a szivárvány leírására.
Cserti József
Eötvös Egyetem, Komplex Rendszerek Fizikája Tanszék