Fizikai Szemle honlap |
Tartalomjegyzék |


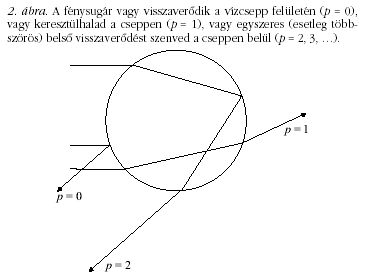
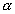 a beesési szög,
a beesési szög, 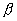 a törési szög, és n az anyag
törésmutatója.1
A szivárvány jelenségének irodalma óriási. Bevezetésként,
a téma egyik kiemelkedő szakértője, H. Moysés
Nussenzveig népszerűsítő cikkét [6], Honyek Gyula Középiskolai
Matematikai és Fizikai Lapokban megjelent
írását [7] és Czelnai Rudolf meteorológusképzésben használt
egyetemi jegyzetét [8] ajánlhatjuk az olvasónak. A
matematikai részletek iránt érdeklődők számára a leideni
professzor, Hendrik Christoffel van de Hulst [9] klasszikusnak
számító könyvét, Milton Kerker [10] fényszórásról
írt könyvét és John A. Adam [11] hosszú, összefoglaló
cikkét javasoljuk. A szivárványnak a tudománnyal és a
művészettel való kapcsolatáról Raymond L. Lee és Alistair
B. Fraser közelmúltban megjelent és gazdagon illusztrált
könyvét [12] ajánljuk.
A továbbiakban áttekintjük a szivárvány fizikájának
legfontosabb elemeit, és igyekszünk nyomon követni a
jelenség megértésében történeti szempontból is mérföldkőnek
számító elméleti eredményeket. Elsőként részletesen
ismertetjük Descartes geometriai optikán alapuló
elméletét. A következő, II. részben a polarizáció szerepét,
Thomas Young interferenciaelméletét, majd George
Biddell Airy elméletét taglaljuk. A dolgozat III. részében
vázoljuk a múlt század elején Gustav Mie által kidolgozott
legpontosabb elméletet, illetve a modern matematikai
módszerekkel kapott közelítő eredményekről adunk
rövid áttekintést, beleértve a témához szorosan kapcsolódó
koszorú- és glóriajelenséget is. A következő fejezetben
szólunk a szivárvány és a kvantummechanika kapcsolatáról.
Végül az összefoglalóban további, a témával
kapcsolatos kérdéseket említünk meg.
Megjegyezzük, hogy a cikk ábráinak egy része a Mathematica
programmal készült, és eredetileg színesek. Az
érdeklődők [13] internetcímen tekinthetik meg az eredeti
ábrákat.
Geometriai optikai leírás
a törési szög, és n az anyag
törésmutatója.1
A szivárvány jelenségének irodalma óriási. Bevezetésként,
a téma egyik kiemelkedő szakértője, H. Moysés
Nussenzveig népszerűsítő cikkét [6], Honyek Gyula Középiskolai
Matematikai és Fizikai Lapokban megjelent
írását [7] és Czelnai Rudolf meteorológusképzésben használt
egyetemi jegyzetét [8] ajánlhatjuk az olvasónak. A
matematikai részletek iránt érdeklődők számára a leideni
professzor, Hendrik Christoffel van de Hulst [9] klasszikusnak
számító könyvét, Milton Kerker [10] fényszórásról
írt könyvét és John A. Adam [11] hosszú, összefoglaló
cikkét javasoljuk. A szivárványnak a tudománnyal és a
művészettel való kapcsolatáról Raymond L. Lee és Alistair
B. Fraser közelmúltban megjelent és gazdagon illusztrált
könyvét [12] ajánljuk.
A továbbiakban áttekintjük a szivárvány fizikájának
legfontosabb elemeit, és igyekszünk nyomon követni a
jelenség megértésében történeti szempontból is mérföldkőnek
számító elméleti eredményeket. Elsőként részletesen
ismertetjük Descartes geometriai optikán alapuló
elméletét. A következő, II. részben a polarizáció szerepét,
Thomas Young interferenciaelméletét, majd George
Biddell Airy elméletét taglaljuk. A dolgozat III. részében
vázoljuk a múlt század elején Gustav Mie által kidolgozott
legpontosabb elméletet, illetve a modern matematikai
módszerekkel kapott közelítő eredményekről adunk
rövid áttekintést, beleértve a témához szorosan kapcsolódó
koszorú- és glóriajelenséget is. A következő fejezetben
szólunk a szivárvány és a kvantummechanika kapcsolatáról.
Végül az összefoglalóban további, a témával
kapcsolatos kérdéseket említünk meg.
Megjegyezzük, hogy a cikk ábráinak egy része a Mathematica
programmal készült, és eredetileg színesek. Az
érdeklődők [13] internetcímen tekinthetik meg az eredeti
ábrákat.
Geometriai optikai leírás
Tekintsük a 3. ábrának megfelelő R sugarú, n törésmutatójú
vízcseppbe

 ütközési paraméterrel vízszintes
irányból érkező fénysugár menetét a főszivárványra (p =2)!
A beesés szögére igaz, hogy 0° <
ütközési paraméterrel vízszintes
irányból érkező fénysugár menetét a főszivárványra (p =2)!
A beesés szögére igaz, hogy 0° < 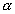 < 90°. Az ábra
alapján világos, hogy
< 90°. Az ábra
alapján világos, hogy 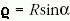 , másrészt a P pontban az
(1) Snellius-Descartes-törvény szerint:
, másrészt a P pontban az
(1) Snellius-Descartes-törvény szerint: 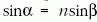 . A
vízcseppbe bemenő és abból kilépő fénysugarak közti
eltérülés szöge (továbbiakban szórási szögnek nevezzük):
. A
vízcseppbe bemenő és abból kilépő fénysugarak közti
eltérülés szöge (továbbiakban szórási szögnek nevezzük):
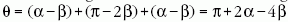 . A Napból jövő
és a szemünkbe érkező fénysugarak közti szög:
. A Napból jövő
és a szemünkbe érkező fénysugarak közti szög: 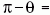
 (Bacon kísérleteiben ezt a szöget mérte ki). Teljesen
hasonló számítással kapható a szórási szög abban az
általános esetben is, amikor a vízcsepp belső falán a fénysugár
többször visszaverődik. Könnyen belátható, hogy a
szórási szög p -1 számú belső visszaverődés esetén:
(Bacon kísérleteiben ezt a szöget mérte ki). Teljesen
hasonló számítással kapható a szórási szög abban az
általános esetben is, amikor a vízcsepp belső falán a fénysugár
többször visszaverődik. Könnyen belátható, hogy a
szórási szög p -1 számú belső visszaverődés esetén: 
 .
Az (1) egyenletet felhasználva a
.
Az (1) egyenletet felhasználva a  szöget kifejezhetjük a
szöget kifejezhetjük a

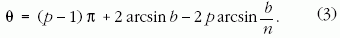
 nagyobb lehet
nagyobb lehet 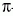 -nél,
ezért a gyakorlati számításoknál a
-nél,
ezért a gyakorlati számításoknál a  szöget a (0,
szöget a (0,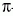 ) intervallumba
képezzük:
) intervallumba
képezzük:
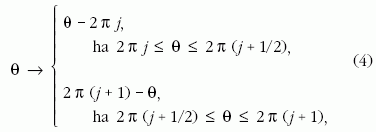
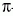 ) intervallumba.)
A 4. ábra a
) intervallumba.)
A 4. ábra a  szórási szögeknek a b ütközési paramétertől való függését
mutatja p = 0, 1, 2, 3 értékekre. Két fontos megállapítás
tehető az ábra alapján. Egyrészt látható, hogy p > 0 esetén
szórási szögeknek a b ütközési paramétertől való függését
mutatja p = 0, 1, 2, 3 értékekre. Két fontos megállapítás
tehető az ábra alapján. Egyrészt látható, hogy p > 0 esetén
 értéke b = 1-nél (azaz a vízcsepp felszínéhez érintőlegesen
érkező fénysugár esetén) zérustól különböző érték:
értéke b = 1-nél (azaz a vízcsepp felszínéhez érintőlegesen
érkező fénysugár esetén) zérustól különböző érték:

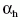 a vízre vonatkozó teljes visszaverődés határszöge,
azaz sin
a vízre vonatkozó teljes visszaverődés határszöge,
azaz sin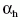 = 1/n. Későbbiekben látni fogjuk, hogy a
= 1/n. Későbbiekben látni fogjuk, hogy a
 * szögnek fontos szerepe lesz a szórási
hatáskeresztmetszet számításában és az interferenciajelenségek vizsgálatában
is.
* szögnek fontos szerepe lesz a szórási
hatáskeresztmetszet számításában és az interferenciajelenségek vizsgálatában
is.

 szórási szögnek p > 1 esetén szélsőértéke van
b függvényében. A továbbiakban szükségünk van
szórási szögnek p > 1 esetén szélsőértéke van
b függvényében. A továbbiakban szükségünk van  -nak a
b szerinti első deriváltjára, melyet könnyen megkaphatunk
a (3) képletből:
-nak a
b szerinti első deriváltjára, melyet könnyen megkaphatunk
a (3) képletből:

 /db = 0 feltételből adódik:
/db = 0 feltételből adódik:
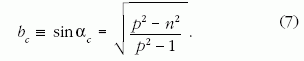
 beesési szögben érkezik
a vízcsepphez. Ezt a speciális sugármenetet az irodalomban
szokásos módon, és Descartes tiszteletére, nevének
latin megfelelője szerint Cartesius-sugárnak nevezzük,
és a c index is a Cartesius névre utal. Kiszámíthatjuk
a
beesési szögben érkezik
a vízcsepphez. Ezt a speciális sugármenetet az irodalomban
szokásos módon, és Descartes tiszteletére, nevének
latin megfelelője szerint Cartesius-sugárnak nevezzük,
és a c index is a Cartesius névre utal. Kiszámíthatjuk
a  szórási szöget is ezen szélsőértékhelyen:
szórási szöget is ezen szélsőértékhelyen:

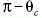 - szögeket. Látható, hogy fő- és mellékszivárványban
a színek sorrendje fordított. Csak érdekességképpen
jegyezzük meg, hogy az 1. ábrán látható
mellékszivárványnál a vízcseppen belül a Cartesius-sugár
nagyon jó közelítéssel egy négyzet oldalélei mentén halad.
- szögeket. Látható, hogy fő- és mellékszivárványban
a színek sorrendje fordított. Csak érdekességképpen
jegyezzük meg, hogy az 1. ábrán látható
mellékszivárványnál a vízcseppen belül a Cartesius-sugár
nagyon jó közelítéssel egy négyzet oldalélei mentén halad.
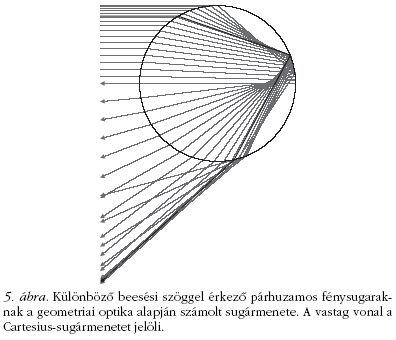

 és
és  + d
+ d szög közé szóródik! (Az adott szögtartományba
szóródó energiát a szórócentrum köré rajzolt egységnyi
sugarú gömb felületén vett intenzitással mérik.) Ha a bejövő
párhuzamos fénysugarakra merőleges keresztmetszeten,
egységnyi felületen áthaladó nyaláb intenzitása
S0, akkor a
szög közé szóródik! (Az adott szögtartományba
szóródó energiát a szórócentrum köré rajzolt egységnyi
sugarú gömb felületén vett intenzitással mérik.) Ha a bejövő
párhuzamos fénysugarakra merőleges keresztmetszeten,
egységnyi felületen áthaladó nyaláb intenzitása
S0, akkor a  irányba
szóródó sugarak differenciális hatáskeresztmetszete
definíció szerint
irányba
szóródó sugarak differenciális hatáskeresztmetszete
definíció szerint 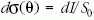 . Ez területdimenziójú
mennyiség. Először tegyük fel, hogy a
. Ez területdimenziójú
mennyiség. Először tegyük fel, hogy a  szórási szögés a ütközési paraméter között kölcsönösen
egyértelmű a kapcsolat, azaz
szórási szögés a ütközési paraméter között kölcsönösen
egyértelmű a kapcsolat, azaz  az ütközési paraméter
monoton függvénye.2 A
az ütközési paraméter
monoton függvénye.2 A 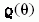 és
és
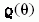 +
+  sugarak
által határolt körgyűrűn áthaladó fénynyaláb intenzitása
sugarak
által határolt körgyűrűn áthaladó fénynyaláb intenzitása
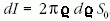 . Így a differenciális hatáskeresztmetszet
. Így a differenciális hatáskeresztmetszet
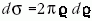 , amely kifejezhető a szóródás
, amely kifejezhető a szóródás  szögével,
vagy a
szögével,
vagy a 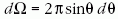 térszöggel:
térszöggel:
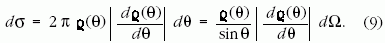
 derivált abszolút értéke szerepel, figyelembe
véve, hogy a derivált negatív is lehet. Ha a
derivált abszolút értéke szerepel, figyelembe
véve, hogy a derivált negatív is lehet. Ha a 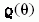 többértékű függvény (mint például a szivárványnál), akkor
a függvény egyes ágainak megfelelően, külön-külön
kell kiszámítani az egyes járulékokat a differenciális hatáskeresztmetszethez.
Általában a
többértékű függvény (mint például a szivárványnál), akkor
a függvény egyes ágainak megfelelően, külön-külön
kell kiszámítani az egyes járulékokat a differenciális hatáskeresztmetszethez.
Általában a  szórási szöget ismerjük a
szórási szöget ismerjük a
 ütközési paraméter függvényében. Ezért először a (9)
képlet szerint meg kell határozni a
ütközési paraméter függvényében. Ezért először a (9)
képlet szerint meg kell határozni a 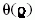 függvény inverzét,
azaz a
függvény inverzét,
azaz a 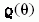 függvényt, majd ennek deriváltját.
függvényt, majd ennek deriváltját.
Vizsgáljuk a főszivárvány (p = 2) esetét!3 A (3) egyenletben
megadott
 függvény inverzét algebrai átalakítások
után a következő egyenletből kaphatjuk meg:
függvény inverzét algebrai átalakítások
után a következő egyenletből kaphatjuk meg:

 -re, és két pozitív
gyöke van (a másik kettő negatív gyök). Jelöljük az így kapott
inverz függvényt
-re, és két pozitív
gyöke van (a másik kettő negatív gyök). Jelöljük az így kapott
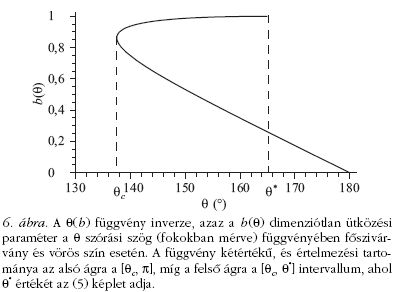
inverz függvényt 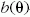 -val! A függvény
kétértékű, alakját a
6. ábra mutatja.4 A
-val! A függvény
kétértékű, alakját a
6. ábra mutatja.4 A 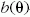 függvény
függvény  szerinti deriváltja - az inverz függvény deriválásának megfelelő szabály szerint -
a (6) egyenletben adott derivált reciproka. A
szerinti deriváltja - az inverz függvény deriválásának megfelelő szabály szerint -
a (6) egyenletben adott derivált reciproka. A 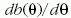 derivált
értéke a
derivált
értéke a 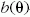 függvény két ágán különböző, sőt ellentétes
előjelűek (ezért kell venni az abszolút értéket a (9)
képletben). Így a differenciális hatáskeresztmetszethez
külön-külön adódnak járulékok az egyes ágakból.
Világos, hogy a
függvény két ágán különböző, sőt ellentétes
előjelűek (ezért kell venni az abszolút értéket a (9)
képletben). Így a differenciális hatáskeresztmetszethez
külön-külön adódnak járulékok az egyes ágakból.
Világos, hogy a 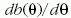 derivált a
derivált a
 =
= 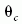 helyen
szinguláris (végtelen értéket vesz fel), és így a differenciális
hatáskeresztmetszet ebben az irányban végtelenné
válik. Ez az oka, hogy a szórt fényt ebben a
helyen
szinguláris (végtelen értéket vesz fel), és így a differenciális
hatáskeresztmetszet ebben az irányban végtelenné
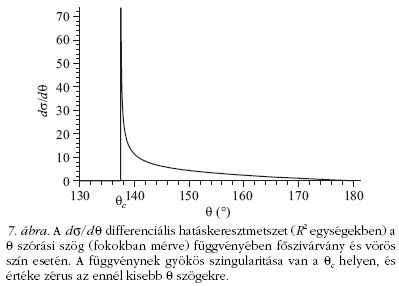
válik. Ez az oka, hogy a szórt fényt ebben a 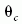 szögben
látjuk a legerősebbnek. Vörös színre a differenciális hatáskeresztmetszet
a 7. ábrán látható. Megjegyezzük,
hogy a hatáskeresztmetszetben fellépő szingularitás gyökös
jellegű, azaz
szögben
látjuk a legerősebbnek. Vörös színre a differenciális hatáskeresztmetszet
a 7. ábrán látható. Megjegyezzük,
hogy a hatáskeresztmetszetben fellépő szingularitás gyökös
jellegű, azaz

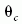 közelében. Természetesen a teljes
hatáskeresztmetszet, azaz az
közelében. Természetesen a teljes
hatáskeresztmetszet, azaz az
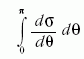
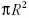 geometriai keresztmetszettel.
Matematikailag az integrál a gyökös szingularitás miatt
lesz véges. Teljesen hasonló gondolatmenet alapján belátható,
hogy mellékszivárványra
geometriai keresztmetszettel.
Matematikailag az integrál a gyökös szingularitás miatt
lesz véges. Teljesen hasonló gondolatmenet alapján belátható,
hogy mellékszivárványra 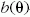 inverz függvény deriváltja a p = 3-nak megfelelő
inverz függvény deriváltja a p = 3-nak megfelelő 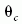 értéknél válik végtelenné, és így a hatáskeresztmetszet is.
Összegezve, a szivárvány színeit azokban az irányokban
látjuk legerősebbnek, amelyekben az egyes színekhez
tartozó differenciális hatáskeresztmetszetek szingulárisak.
Ezeket a szögeket a fő- és mellékszivárvány esetében
a (8) képletből számolhatjuk ki, és numerikus értékei
1. táblázatban találhatók. Mivel a (3) képletben adott
értéknél válik végtelenné, és így a hatáskeresztmetszet is.
Összegezve, a szivárvány színeit azokban az irányokban
látjuk legerősebbnek, amelyekben az egyes színekhez
tartozó differenciális hatáskeresztmetszetek szingulárisak.
Ezeket a szögeket a fő- és mellékszivárvány esetében
a (8) képletből számolhatjuk ki, és numerikus értékei
1. táblázatban találhatók. Mivel a (3) képletben adott
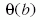 függvénynek csak p > 1 mellett van szélsőértéke,
szivárványt csak ekkor figyelhetünk meg. A magasabb
rend? szivárványokra (p > 3) a differenciális hatáskeresztmetszetet
az előbbiekhez hasonlóan, általában csak
numerikusan határozhatjuk meg.
Itt jegyezzük meg, hogy a 4. ábra alapján főszivárványra,
adott színű fényre a
függvénynek csak p > 1 mellett van szélsőértéke,
szivárványt csak ekkor figyelhetünk meg. A magasabb
rend? szivárványokra (p > 3) a differenciális hatáskeresztmetszetet
az előbbiekhez hasonlóan, általában csak
numerikusan határozhatjuk meg.
Itt jegyezzük meg, hogy a 4. ábra alapján főszivárványra,
adott színű fényre a  szórási
szög nagyobb a p = 2-nek megfelelő
szórási
szög nagyobb a p = 2-nek megfelelő 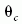 -nél,
míg a mellékszivárvány esetén a
szórási szög kisebb a p = 3-nak megfelelő
-nél,
míg a mellékszivárvány esetén a
szórási szög kisebb a p = 3-nak megfelelő 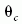 -nél.
Mivel
-nél.
Mivel 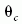 (p = 3) <
(p = 3) < 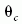 (p = 2),
e két szög közti irányokból az adott
szín? fény sem a főszivárványból, sem a mellékszivárványból
nem juthat a szemünkbe. A két szög közti irányban,
a fő- és mellékszivárvány között egy sötét tartomány
alakul ki, a bevezetőben említett Alexander-féle sötét sáv.
Az 1. táblázatból látható, hogy
(p = 2),
e két szög közti irányokból az adott
szín? fény sem a főszivárványból, sem a mellékszivárványból
nem juthat a szemünkbe. A két szög közti irányban,
a fő- és mellékszivárvány között egy sötét tartomány
alakul ki, a bevezetőben említett Alexander-féle sötét sáv.
Az 1. táblázatból látható, hogy 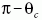 értéke főszivárvány
esetén vörös színre a legnagyobb, mellékszivárványnál
pedig vörös színre a legkisebb. Így az 1. táblázat numerikus
adataival az Alexander-féle sötét sáv a 42,5° és az
50,1° szögek közti irányban látható.
Végül fontos hangsúlyozni, hogy a Descartes-féle elmélet
szerint a szórt fény intenzitása sem a vízcsepp méretétől,
sem a fény hullámhosszától nem függ. A szivárvány
jelenségének megértésében továbblépés Descartes
után közel kétszáz évvel következett be. Az új elméletekben
a fénynek korábban ismeretlen tulajdonsága, a hullámtermészete
kap alapvető szerepet. Ezek az elméletek,
a szivárvány pontosabb leírásán túl, nagy hatással voltak
az egész optika tudományára is. A következő fejezetekben
a szivárványnak a fény hullámtermészetén alapuló
elméleteit ismertetjük.
Irodalom
1.
http://www.sundog.clara.co.uk/rainbows/bows.htm
értéke főszivárvány
esetén vörös színre a legnagyobb, mellékszivárványnál
pedig vörös színre a legkisebb. Így az 1. táblázat numerikus
adataival az Alexander-féle sötét sáv a 42,5° és az
50,1° szögek közti irányban látható.
Végül fontos hangsúlyozni, hogy a Descartes-féle elmélet
szerint a szórt fény intenzitása sem a vízcsepp méretétől,
sem a fény hullámhosszától nem függ. A szivárvány
jelenségének megértésében továbblépés Descartes
után közel kétszáz évvel következett be. Az új elméletekben
a fénynek korábban ismeretlen tulajdonsága, a hullámtermészete
kap alapvető szerepet. Ezek az elméletek,
a szivárvány pontosabb leírásán túl, nagy hatással voltak
az egész optika tudományára is. A következő fejezetekben
a szivárványnak a fény hullámtermészetén alapuló
elméleteit ismertetjük.
Irodalom
1.
http://www.sundog.clara.co.uk/rainbows/bows.htm
2. http://www.sundog.clara.co.uk/rainbows/supers.htm
3. RENÉ DESCARTES: Discours de la Méthode - 1637, további utalások
találhatók még[5]-ben
4. MÁTRAI TIBOR: Gyakorlati spektroszkópia - Műszaki Könyvkiadó, Budapest, 1963
5. SIMONYI KÁROLY: A fizika kultúrtörténete - Gondolat Kiadó, Budapest,
1986 (3. kiadás)
6. H.M. NUSSENZVEIG: The theory of the rainbow - Scientific American
236 (1977) 116-127
7. HONYEK GYULA: A szivárvány - Középiskolai Matematikai és Fizikai
Lapok 1991/1 33-37
6. H.M. NUSSENZVEIG: The theory of the rainbow - Scientific American
236 (1977) 116-127
7. HONYEK GYULA: A szivárvány - Középiskolai Matematikai és Fizikai
Lapok 1991/1 33-37
8. CZELNAI RUDOLF: Bevezetés a meteorológiába I. Légkörtani alapismeretek
- Egyetemi jegyzet, Eötvös Loránd Tudományegyetem,
Természettudományi Kar, Tankönyvkiadó, Budapest, 1979
9. H.C. VAN DE HULST: Light scattering by small particles - New York,
John Wiley & Sons, Inc. 1957; New York, Dover 1981
10. M. KERKER: The scattering of light - Academic Press, New York and
London, 1969
11. JOHN A. ADAM: The mathematical physics of rainbows and glories -
Physics Reports 356 (2002) 229-365
12. R.L. LEE, JR., A.B. FRASER: The rainbowbridge: rainbows in art,
myth and science - Pennsylvania State University, Philadelphia,
USA, 2001
13. http://www.kfki.hu/fszemle
http://complex.elte.hu/cserti/Szivarvany.pdf
14. J.D. WALKER: Multiple rainbows from single drops of water and
other liquids - American Journalof Physics 44 (1976) 421-433
15. L.D. LANDAU, E.M. LIFSIC: Elméleti fizika I (Mechanika) -
Tankönyvkiadó,
Budapest, 1974
_________________________________
1 Megjegyezzük, hogy az angol nyelvű irodalomban ezt a törvényt
egyszerűen csak Snell-törvénynek nevezik. Nem lehet bizonyosan
tudni, hogy Descartes ismerte-e a leideni egyetem professzora, Willebrord
Snell eredményeit, melyet ő maga már 1620-ban tanított az egyetemen.
Tény, hogy a töréstörvényt Descartes publikálta először, de nem
említi Snell munkásságát. Descartes tudományos tevékenységéről bővebb
betekintést például Simonyi Károly művéből kaphatunk [5].
2 Szórási jelenségeknél gyakran fordul elő, hogy ez a függvény nem
monoton. Például szivárványnál (p > 1) a 4.
ábra alapján jól látható,
hogy éppen ez a helyzet. Ilyenkor a függvényt felbontjuk monoton
függvények ágaira.
3 Itt jegyezzük meg, hogy p = 0 és p = 1 mellett a hatáskeresztmetszet
analitikusan kiszámolható, a részletek megtalálhatók a [15] könyvben a
73. és a 80. oldalon.
4 A 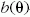 függvényt geometriailag a 4. ábrán látható
függvényt geometriailag a 4. ábrán látható
 (b) függvénynek
a 45°-os egyenesre való tükrözésével kaphatjuk meg.
(b) függvénynek
a 45°-os egyenesre való tükrözésével kaphatjuk meg.